|
| Conic
Sections |
|
|
|
|
Circle
and Line
|
Equation of a tangent at a point
of a translated circle
|
|
Equation of a tangent at a point
of a circle, examples
|
|
|
|
|
|
|
| Equation of a tangent at a point
of a translated circle (x
-
p)2 + (y -
q)2 = r2 |
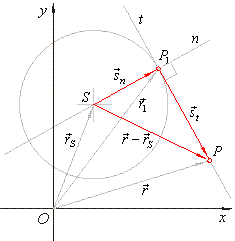
| The direction vector of the tangent at the point P1(x1, y1), of a circle whose center is at the point
S(p,
q), and the direction vector of the normal, are perpendicular, so their scalar product is zero. |
| Points,
O,
S,
P1
and P
in the right figure, determine vectors, |
 |
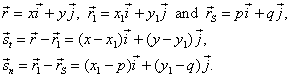| Since |
 |
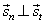their scalar product is zero, that is |
|
 |
|
 |
|
 |
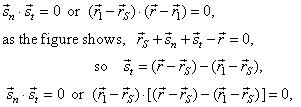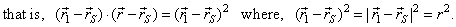| Therefore, |
 |
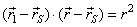is
vector equation of a tangent at the point of a translated
circle, |
|
| or,
when this scalar product is written in the component form, |
(x1
-
p) · (x
-
p) + (y1
-
q)
· (y
-
q) = r2 |
|
| it
represents the equation of the tangent at the point P1
(x1, y1), of a circle whose center is at
S(p,
q). |
|
Example:
Find the angle formed by tangents drawn at points of intersection of a line
x -
y + 2 = 0 and
the circle x2
+ y2 = 10. |
| Solution:
Solution of the system of equations gives coordinates of the intersection points, |
 |
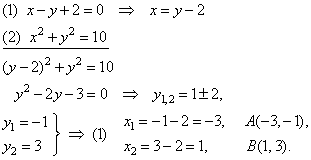| Plug coordinates of
A
and B
into equation of the tangent: |
 |
|
 |
|
 |
|
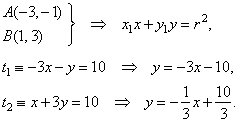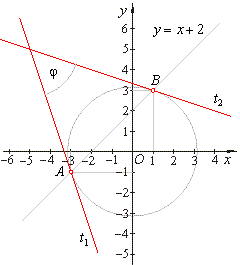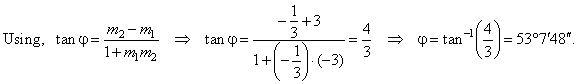| Example:
At intersections of a line x -
5y + 6 = 0 and the circle
x2
+ y2 -
4x + 2y
-
8 = 0 drown are tangents,
find the area of the triangle formed by the line and the tangents. |
| Solution:
Intersections of the line and the circle are also tangency points. Solutions of the system of
equations are coordinates of the tangency points, |
| (1)
x -
5y + 6 = 0 => x =
5y -
6 =>
(2) |
| (2)
x2
+ y2 -
4x + 2y
-
8 = 0 |
| |
| (5y
- 6)2
+ y2 -
4(5y - 6) + 2y
-
8 = 0 |
| y2 -
3y + 2 = 0,
=>
y1 =
1 and y2
=
2 |
|
x1 =
5 · 1 - 6
= -1,
=> A(-1,
1), |
|
x2 =
5 · 2 - 6
=
4,
=> B(4,
2). |
| Rewrite
the equation of the circle into standard form, |
| (x
-
p)2 + (y -
q)2 = r2 |
|
 |
|
|
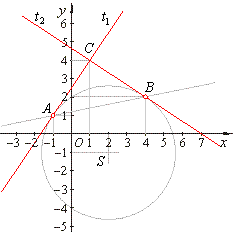x2
+ y2 -
4x + 2y
-
8 = 0
=>
(x
-
2)2 + (y +
1)2 = 13, thus
S(2,
-1) and
r = Ö13. |
| Plug
tangency points A and
B
into equation of the tangent, |
| A( -1,
1) and B(4,
2) =>
(x1
-
p) · (x
-
p) + (y1
-
q)
· (y
-
q) = r2 |
| (-1
-
2) · (x
- 2) + (1 +
1)
· (y
+
1) =
13
=>
t1 ::
-
3x + 2y -
5 = 0, |
| (4
-
2) · (x
- 2) + (2 +
1)
· (y
+
1) =
13
=>
t2 ::
2x +
3y -
14 = 0. |
| Solution of the system of equations of tangents determines the third vertex
C
of the triangle, |
|
-
3x + 2y -
5 = 0 Tangents are perpendicular
since their slopes satisfy the condition, m1
=
- 1/m2. |
|
2x + 3y -
14 = 0,
C(1, 4) |
| |
| The triangle
ABC is right isosceles, whose area
A =
1/2 · AC 2
=
1/2 · Ö(22
+ 32)2
=
13/2 square units. |
|
|
|
|
|
|
|
