|
|
Series |
 Tests
for convergence
Tests
for convergence |
|
Ratio
test |
|
Root
test or Cauchy's root test |
|
|
|
|
|
|
| The
ratio test |
| The test
for whether a series is absolutely convergent by testing the limit of the absolute
value of
the ratio of
successive
terms of the series is called the ratio test. |
| |
(1)
If |
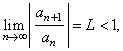 |
then
the series |
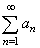 |
is
absolutely
convergent. |
|
|
| |
(2)
If |
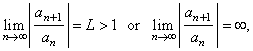 |
then
the series |
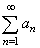 |
is
divergent.
|
|
|
| |
(3)
If |
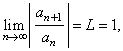 |
then
the test is inconclusive,
i.e.,
gives
no information. |
|
|
|
| Example: Examine
whether the series |
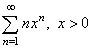 |
converges
or diverges. |
|
| Solution: Since, |
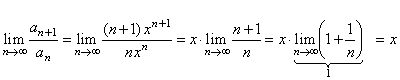 |
|
|
| the
series converges if 0
< x < 1. |
|
| Example: Determine
whether the series |
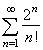 |
converges
or diverges. |
|
| Solution: Since, |
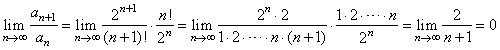 |
|
| therefore L
< 1 and the series converges. |
| If
the given series has a factorial in the nth
term expression, the ratio test
should be used. |
|
| Example: Let
show that the logarithmic series |
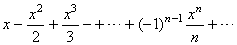 |
converges. |
|
| Solution: |
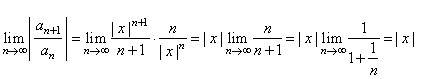 |
|
| thus, the series
converges
for x < 1.
The sum of the series |
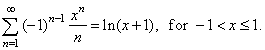 |
|
|
|
Root
test or Cauchy's root test |
| The test
for whether a series |
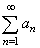 |
of
positive terms is absolutely
convergent by considering; |
|
| |
(1)
If |
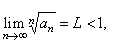 |
then
the series |
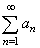 |
is
absolutely
convergent. |
|
|
| |
(2)
If |
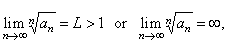 |
then
the series |
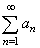 |
is
divergent.
|
|
|
| |
(3)
If |
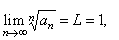 |
then
the test is inconclusive,
i.e.,
gives
no information. |
|
|
|
| Example: Determine
whether the series |
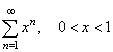 |
converges
or diverges. |
|
| Solution: The
given geometric series converges since |
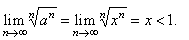 |
|
|
|
| Example: Let
show that the series |
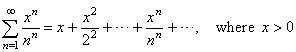 |
converges. |
|
| Solution: The
series converges since |
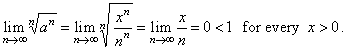 |
|
|
|
| Example: Test
the series |
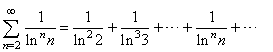 |
for
convergence. |
|
| Solution: The
series converges since |
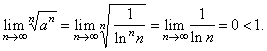 |
|
|
| We
use
the root test when the entire nth
term expression is raised to some power of n. |
|
|
|
|