|
|
Series |
 Tests
for convergence
Tests
for convergence |
|
Comparison
test |
|
Limit
comparison test |
|
Ratio
test |
|
|
|
|
|
|
| Tests
for convergence |
| Comparison
test |
| A
series of positive terms converges if its terms, starting from the first
or one of the further terms, are not greater
than terms of the same index of a known convergent series of positive
terms. |
|
| Suppose
that |
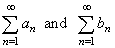 |
are
series of positive terms. Then |
|
| |
(1)
If |
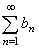 |
is
convergent and an
< bn for all n,
then |
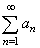 |
is
also convergent. |
|
|
| |
(2)
If |
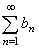 |
is
divergent and an
> bn for all n,
then |
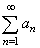 |
is
also divergent. |
|
|
|
| Example: Let
prove that the series |
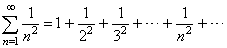 |
converges. |
|
| Solution:
Since
n2 > (n
-
1)n
then |
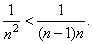 |
In previous section was shown that the series |
|
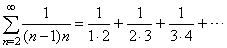 |
| converges
and its sum s
= 1
therefore, by the comparison test, also converges the series |
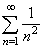 |
and
the |
|
| sum
of which |
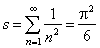 |
as
Euler revealed (in 1736). |
|
| Recall
that the harmonic series, i.e., the series of the
reciprocals of natural numbers diverges while the series of
the reciprocals of squares of natural numbers converges. The reason is,
the terms of the reciprocals of squares
decrease faster then the terms of the harmonic series. |
|
| The
limit
comparison test |
| Suppose |
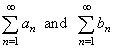 |
are series of
positive
terms. If |
|
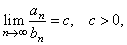 |
| then
the series are either both convergent or both divergent. |
|
| Example: Let
prove that the series |
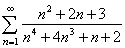 |
converges. |
|
| Solution: |
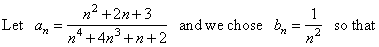 |
|
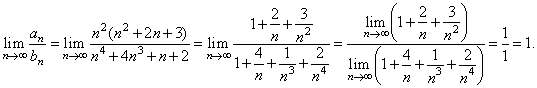 |
| Since
both series are of positive terms, the limit is 1
> 0, and the series bn
= 1/n2 is
convergent then, by the
limit
comparison test given series also converges. |
|
| The
ratio test |
| The test
for whether a series is absolutely convergent by testing the limit of the absolute
value of
the ratio of
successive
terms of the series is called the ratio test. |
| |
(1)
If |
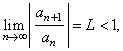 |
then
the series |
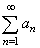 |
is
absolutely
convergent. |
|
|
| |
(2)
If |
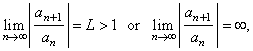 |
then
the series |
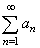 |
is
divergent.
|
|
|
| |
(3)
If |
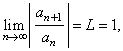 |
then
the test is inconclusive,
i.e.,
gives
no information. |
|
|
|
| Example: Let
show that the series |
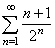 |
converges. |
|
| Solution: Since, |
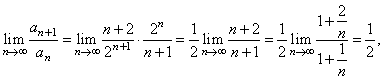 |
the series
converges. |
|
|
| Example: Let
show that the series |
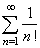 |
converges. |
|
| Solution: |
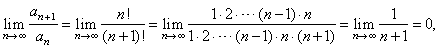 |
|
| thus,
the series
converges. |
|
|
|
|
|
|