|
|
Limits of sequences |
Properties of
convergent sequences |
|
Sandwich
theorem (result) or squeeze rule |
|
Least
upper bound (or supremum, abbrev. lub, sup) and greatest lower bound (infimum, abbrev. glb, inf) |
|
The
definition of the real number e |
|
|
|
|
|
|
|
| Sandwich
theorem (result) or squeeze rule |
| Suppose
that {bn}
is a sequence whose terms are bounded above and below (squeezed between)
by sequences {cn}
and {an}
respectively,
such that |
| an
< bn < cn
for all n
and if an
®
L
and cn
®
L,
then bn
®
L. |
|
| Least
upper bound (or supremum, abbrev. lub, sup) and greatest lower bound (or
infimum, abbrev. glb, inf) |
| Suppose
{an}
is a bounded increasing sequence of real numbers, then the least upper
bound of the set { an
: n
Î
N }
is the limit of {an},
so we write L
= sup an. |
| Proof:
Suppose L
= sup an
then, for
given e
> 0 there exists an integer n0
such that |
|
an0
> L -
e
or L - an0
< e. |
| Since
{an}
is increasing an
> an0
> L -
e
for all n
> n0,
and since L
is the upper bound of the sequence then, L
>
an
for every n,
therefore |
| |
L
-
an
| = L -
an
< L - an0
< e
for all n
> n0
that is, an
®
L. |
| Similarly,
if {an}
is a bounded decreasing sequence of real numbers, then the greatest
lower bound of the set
{ an
: n
Î
N }
is the limit of {an},
and we write L
= inf an. |
|
| The
definition of the real number
e |
| We
use the monotonic sequence theorem to prove that the sequence defined
by |
 |
|
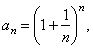| is
increasing and its terms remain less than one fixed number as n
tends to infinity, that is, the sequence converge to the
number e. |
| Recall
the binomial expansion theorem |
 |
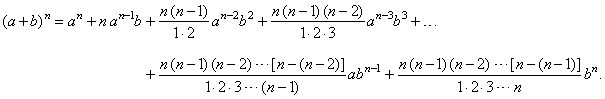| Let
expand an
using the above theorem |
 |
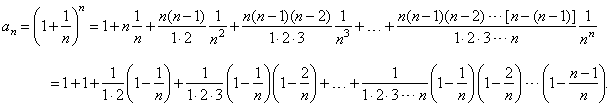| Then,
to prove an+1
> an, that is,
that given is increasing sequence, we can expand an+1
the same way. |
| Observe
that, while passing from n
to n
+ 1, the an+1
expression gets one new positive term and, at the same time, all the
differences in parentheses raised as every subtrahend decreased (i.e., denominators
increased
to n
+ 1). Therefore, since an+1
> an the
sequence is increasing. |
| To
show that all terms of the sequence are less than a fixed number M
we will evaluate the quantity an
on a suitable
way. |
| If
we omit second term (consisting 1/n)
in every parenthesis,
they increase, hence |
 |
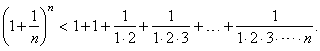| If
instead of the factors, 3,
4,
. . . , n
in the denominators, starting from the second, we substitute 2,
the denominators
decreased so the fractions increased, thus |
 |
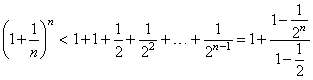| since
applied is the formula for the sum of the finite geometric series whose
ratio is 1/2
and the first term 1. |
| As
the right side still depends on n,
to get an expression independent of n,
the one which holds to all terms, drop
the term 1/2n
in the numerator of the right side, what increases the numerator, such
that the final result is |
 |
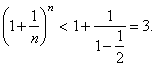| Therefore,
as all terms of the sequence are less than M = 3 then, the sequence has
a limit that is not greater
than 3. |
| Let
write few terms of the sequence to show how slowly it increases, |
 |
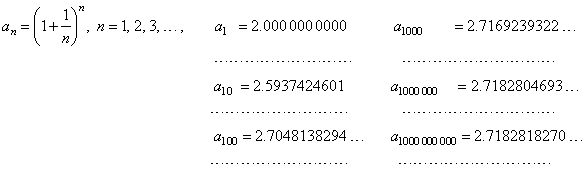| So,
we finally write |
 |
|
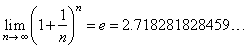