|
|
Limits of sequences |
 Properties of
convergent sequences
Properties of
convergent sequences |
|
The limit value is
exclusively determined by the behavior of the terms in its close
neighborhood |
|
Bounded sequences |
|
Every convergent sequence is bounded |
|
Increasing,
decreasing, monotonic sequence |
|
Every subsequence of
a convergent sequence
converges to the same limit |
|
Every
bounded monotonic sequence is convergent example |
|
|
|
|
|
|
|
| Properties of
convergent sequences |
|
| Bounded
sequences |
| A
sequence is bounded above if there is a number M
such that an
< M for all n. |
|
It is bounded below if there is
a number m
such that an
> m for all n. |
| If
a sequence is bounded above and bellow it is called bounded sequence. |
| Thus,
a sequence is bounded if there exist a number M
> 0
such that | an | <
M
for all n. |
| A
sequence which is not bounded is called unbounded. |
|
| b)
From the fact that outside the interval
of the length 2e
lie only finite number of terms of a sequence it follows
that every convergent sequence is bounded, that is |
| there exists
a
number M > 0
such that
| an | <
M
for all n. |
| Therefore, all terms of a convergent sequence can be closed, in the interval
containing finite number of the initial
terms outside the interval 2e,
and in the interval 2e
itself. |
| Any
convergent sequence is bounded (both above and below). |
|
| c)
If
{an}
is a convergent sequence, then every subsequence of that sequence
converges to the same limit. |
| Let
from a convergent sequence extracted is infinitely many terms, an1,
an2,
. . . ,
anp,
. . . ,
using any principle, for example
extracted is every other term, then
they make new infinite sequence called subsequence.
Then, the extracted
subsequence
converges to the same limit as the original sequence. |
| That
is, if | an
-
L | < e
for all n >
n0(e),
then | anp
-
L | < e
for all np
>
n0(e) |
|
since the natural numbers np
are contained within n,
and np
®
oo when
n
®
oo
. |
|
| d)
The
limit L
can belong to a sequence but should not. By its definition the limit
does not belong to a
sequence since the definition says, the limit is a value that is
approached increasingly closely by a sequence as n
tends to infinity. |
| e)
Terms
of a sequence which are far
enough can be considered as the approximate value of the limit L. |
| This
way defined is every irrational number as the limit of the two
infinite sequences, {an}
and {bn}
of rational
numbers that satisfies following conditions. |
| 1)
The sequence {an}
is increasing (nondecreasing) and the {bn}
is decreasing (nonincreasing), i.e., |
| a1
<
a2
<
. . . <
an
<
an +
1
<
. . .
and b1
>
b2
>
. . . >
bn
>
bn +
1
>
. . . |
| 2)
None of the terms of {an}
is greater then any of the terms of {bn}, |
| an
<
bn
where n
= 1, 2, 3, .
. . |
| that
is, every number an
lies to the left of every number bn
on the number line. |
| 3)
The difference bn
-
an
of a two terms of the given sequences of the same index n
can become arbitrary
small as n
tends to infinity, |
| lim
(bn
-
an)
= 0 as
n
®
oo |
| as
is shown on the number line below. |
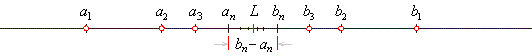 |
| Therefore,
according
to the given conditions the following must hold. |
| There
is only one real number L
determined by these two sequences such that none of the terms of {an}
is
greater then L
(an
<
L)
and that none of the terms of {bn}
is less then L
(bn
>
L). |
| Thus, both sequences,
{an}
and {bn}
approach the
same limit L
from below and above,
i.e., |
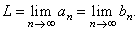 |
| For
example, the circumference of the circle is the limit to which
the circumferences of inscribed and circumscribed
polygons increase and decrease, respectively, as the number of sides
increases to infinity. |
|
| Increasing,
decreasing, monotonic sequence |
|
A sequence is increasing (or strictly increasing) if |
| a1
<
a2
< .
. . <
an
<
an +
1
<
.
. . ,
or an +
1 >
an
for every n. |
|
A sequence is decreasing (or strictly decreasing) if |
| a1
>
a2
>
.
. . >
an
>
an +
1
>
.
. . ,
or an +
1 <
an
for every n. |
|
A sequence is called monotonic (monotone) if it is either increasing or
decreasing. |
|
| Thus,
increasing sequences either,
diverge to +
oo
as n
tends to infinity, written |
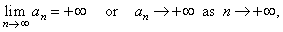 |
| (as,
for example, the sequence of natural numbers) or it is bounded
above, an
<
M for
all n Î
N,
that is
all terms
of
the sequence remain less than a fixed number M. |
| Decreasing sequences
either,
diverge to -
oo
as n
tends to infinity, written |
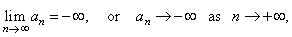 |
| (as,
for example, the sequence -1,
-2,
-3,
.
. .
) or it is bounded
below, an
>
m for
all n Î
N,
that is
all terms of
the sequence remain greater than a fixed number m. |
|
|
| Monotonic
sequence theorem |
| An
increasing sequence, whose all terms are less than a fixed number M,
tends to a finite limit value L
that is
not
greater than M,
therefore |
| if
an +
1
>
an
and
an
<
M, n = 1, 2, 3,
.
. . |
then |
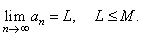 |
|
|
| A
decreasing sequence, whose all terms are greater than a fixed number m,
tends to a finite limit value L
that
is not less than m,
therefore |
| if
an +
1
<
an
and
an
>
m, n = 1, 2, 3,
.
. . |
then |
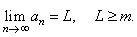 |
|
|
| Thus,
every
bounded monotonic sequence is convergent. |
|
| Example: Prove
that the sequence given by |
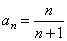 |
is
increasing and bounded. |
|
|
| Solution:
Since |
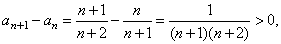 |
|
|
| that
is, an +
1 >
an
for any natural number
n,
therefore the sequence is increasing. |
| By
drawing the first few terms of the sequence on the number line and
examining the nth
term expression as n
tends to infinity, it follows that given sequence is bounded above by 1, |
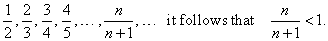 |
| Let
verify that 1 is the limit of the sequence using the definition, |
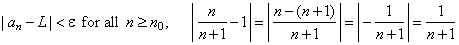 |
| therefore,
as we can make the distance between the nth
term and 1 as small as we wish by choosing n
large
enough, given sequence is convergent. |
|
|
|