|
|
|
|
Sequences
and limits |
 The limit of a sequence
The limit of a sequence |
|
The definition of the limit of a sequence |
|
Convergence of a sequence |
|
Verifying the convergence of a sequence from the definition, examples |
|
|
|
|
|
|
| The limit of a sequence |
|
The definition of the limit of a
sequence |
| A
number L is
called the limit of a sequence {an}
if
for every positive number e there exist a natural number |
| n0
such that if
n
> n0,
then |
an
-
L
|
< e. |
| That
is, a
number L is the limit of a sequence
if the distance between the term an
and L
becomes arbitrary small
by choosing n
large enough (see the examples above). The n0
denotes the value of the index n
starting from which the distance an
-
L
becomes smaller than the given e. |
|
Since the value of n0
depends on the size of e
it is usually written as n0(e). |
|
|
Convergence of a sequence |
| Therefore,
if a sequence {an}
has a limit L
we write |
| |
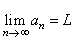 |
or |
an
®
L
as n
®
oo
|
|
|
| and
we say that that a sequence an
has the limit L
as n
tends to infinity. |
| A
sequence {an}
is
convergent if it has a limit. Otherwise, we
say the sequence is divergent. |
| Thus,
the sequences, (3),
(4)
and (5),
from the example above, all converge or tend to the limit 1. |
|
| Example: Let
examine the limit of the sequence (3)
given by |
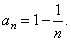 |
|
|
| Solution:
Prove that |
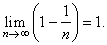 |
|
|
| The
sequence |
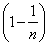 |
tends
to the limit 1
as the distance |
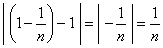 |
can
become |
|
| arbitrary small by
choosing the natural number n
sufficiently large. |
| For
example, if we choose
n = 100
the distance between an
and 1
is 1/n
= 0.01
that is, |
| for
all n > 100
the distance | an
-
1 | < 0.01. |
| Therefore,
n0(e)
= 101 meaning, starting from the 101st
term further, the distance of the remaining terms of the
sequence and 1,
is always less than 0.01. |
|
| Verifying
the convergence of a sequence from the definition, examples |
| Example: Find
the limit of the sequence (2)
given by |
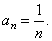 |
|
|
| Solution:
Let
prove that |
 |
|
|
| Using
the definition of limit we must find a natural number
n0(e)
such that | an
-
0 | < e
for all n >
n0. |
| Therefore,
if n >
n0 then
|1/n -
0 | = |1/n | = 1/n < 1/n0 < e. |
| Suppose
we wish to make the difference (or the distance) between the anth
term and
the limit L
to be less than e
= 0.001 = 1/1000. |
| Then,
as 1/n < e
or n
> 1/e
it follows n
> 1000
that is, starting from n0
= 1001
the distance an
-
L becomes smaller than the given e. |
|
| Observe
that the absolute value of terms of the sequences that converge to zero
become arbitrary small as n tends
to infinity that is,
| an
| < e
for all n >
n0(e). |
| For
example such sequences are, |
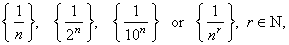 |
therefore |
|
|
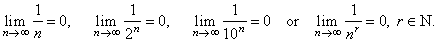 |
|
| The
same way we can prove that the sequence (5)
above,
given by |
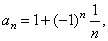 |
converges
to 1. |
|
| As
can be seen on the number line above, the
terms of the sequence alternate from left to right approaching closer and closer to
1 as n
tends
to infinity. |
| That
is, the sequence |
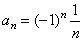 |
alone alternately converges from left to right approaching closer and |
|
| closer to 0 as
n
tends to infinity. |
|
|
Example: Find
the limit of the sequence,
0.9,
0.99, 0.999, . . . , 0.999 . . . 9 . . . , .
. .
|
|
Solution: The
terms of the sequence can be written as
|
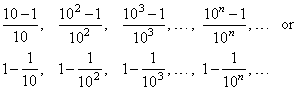 |
| Therefore,
|
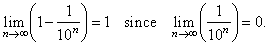 |
|
|
|
|
Example:
The
sequence
|
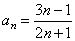 |
has
the limit
3/2,
starting
from which term |
an -
L | < 0.01.
|
|
|
|
Solution: Substitute
given values into the inequality |
an -
L
| < 0.01,
|
|
|
|
Check the result by plugging
n0(e)
= 125
into |
an -
L | < 0.01.
|