|
Limits of
trigonometric functions |
|
Evaluating
trigonometric
limits, examples |
|
Limits of functions
based on the definition of the natural number e |
|
Evaluating
limits of functions
based on the definition of the natural number e |
|
|
|
|
|
|
|
| Evaluating
trigonometric
limits, examples |
| We
use the fundamental limit |
 |
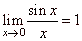and
known trigonometric identities when solving
trigonometric |
|
|
limits.
|
| Example: Evaluate
the limit |
 |
|
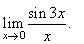| Solution:
|
 |
|
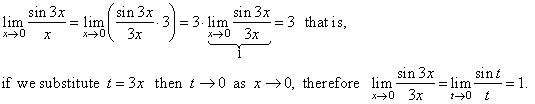| Example: Evaluate
the limit |
 |
|
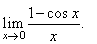| Solution:
Since
cos (a
+ b)
= cosa cosb
-
sina sinb
then cos2a
= cos2a
-
sin2a
= 1 -
2sin2a |
| that
is |
 |
|
|
|
|
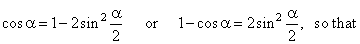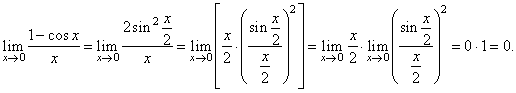
| Example: Evaluate
the limit |
 |
|
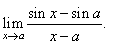| Solution:
We
use the sum to product identity and the fundamental
trigonometric limit, thus |
|
|
|
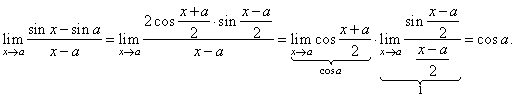
| Example: Evaluate
the limit |
 |
|
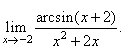| Solution:
If
we substitute arcsin
(x
+ 2) = t
then, |
| x
+ 2 = sin t or
x =
sin t -
2 so that, t
®
0 as
x ®
-2,
therefore |
 |
|
|
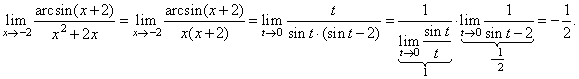Evaluating
limits of functions
based on the definition of the natural number e
|
| Use |
 |
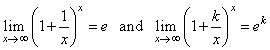to
evaluate limits of the form |
 |
|
|
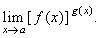| Example: Evaluate
the limit |
 |
|
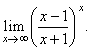| Solution:
|
 |
|
|
|
|
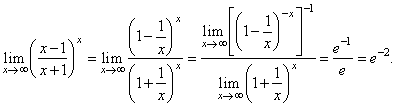| Example: Evaluate
the limit |
 |
|
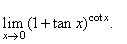| Solution:
|
 |
| |
 |
|
|
|
|
|
|
|
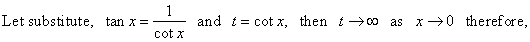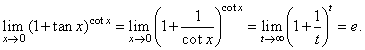