Limits of
rational functions |
|
The limit of a rational function at infinity
containing roots (irrational expressions) |
|
The limit of a rational function at
a point
containing irrational expressions, use of substitution |
|
Evaluating
the limit of a rational function
containing irrational expressions using rationalization |
|
|
|
|
|
|
|
|
|
The limit of a rational function at infinity
containing roots (irrational expressions) |
| We
use the same method we used to
evaluate the limit of a rational function at infinity
that is, isolate and cancel
a common factor of x
from both the numerator and denominator and than find the limit
of the equivalent expression. |
|
| Example: Evaluate
the limit |
 |
|
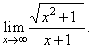| Solution: |
 |
|
|
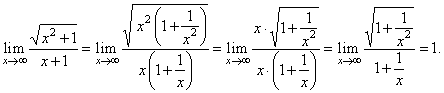| Example: Evaluate
the limit |
 |
|
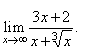| Solution: |
 |
|
|
|
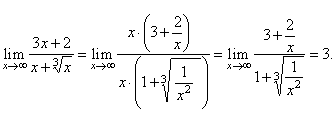The limit of a rational function at a point containing
irrational expressions, use of substitution |
| Use of the method of substitution to avoid the indeterminate form of an expression. |
| Example: Evaluate
the limit |
 |
|
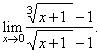| Solution:
Let substitute, x
+ 1 = y6,
then as x
®
0
then y
®
1,
therefore |
|
|
|
| Example: Evaluate
the limit |
 |
|
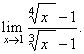| Solution:
Let substitute, x
= y12,
then as x
®
1
then y
®
1,
therefore |
|
|
|
| Evaluating
the limit of a rational function
containing irrational expressions using rationalization |
| To
avoid the
indeterminate form of the irrational expression we rationalize
the numerator or the denominator as
appropriate. |
| Example: Evaluate
the limit |
 |
|
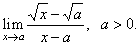| Solution:
Let rationalize
the numerator, |
|
|
|
| Example: Evaluate
the limit |
 |
|
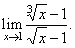| Solution:
Let rationalize
both the numerator
and denominator, |
|
|
