|
Composition
rule
|
|
Limits of
functions
properties use, examples |
 Limits of
rational functions
Limits of
rational functions |
|
Evaluating
the limit of a rational function at infinity |
|
|
|
|
|
|
|
| Limit
properties |
| Assume that |
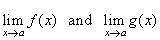 |
exist
and that c
is any constant. Then, |
|
|
|
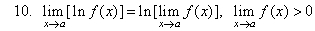 |
|
|
11.
Squeeze rule |
|
If f(x)
< g(x) < h(x)
for all x
in an open interval that contains a,
except possibly at x
= a, |
|
and |
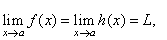 |
|
|
|
then |
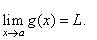 |
|
|
|
|
12.
Composition rule |
|
If f(x)
is continuous at x
= b
and |
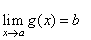 |
|
|
|
then, |
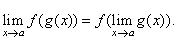 |
|
|
|
| Limits of
functions
properties use, examples |
| Limits
that are commonly used are written below for easy reference, |
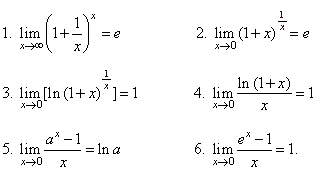 |
|
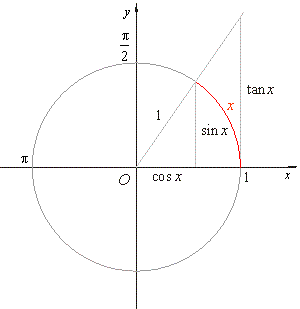
| By
comparing the area of the sector of the arc x
with areas
of the two right triangles, the smaller triangle
with
legs sin x
and cos x,
and the bigger triangle with legs
tan x
and 1, shown on the right figure, we get |
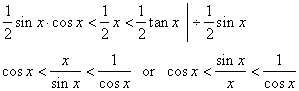 |
| Since
the left and the right side of the last
inequality tend
to the same limit 1, as x
tends to 0 then, applying
the squeeze rule obtained is |
|
|
|
 |
|
| the
fundamental or basic trigonometric limit.
Note
that the arc length x
is measured in radians. |
| Further, |
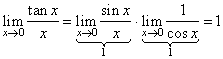 |
|
since both
factors on the right tend to 1, as x
tends to 0, then |
|
|
|
| Limits of
rational
functions |
| A
rational function is the ratio of two polynomial functions |
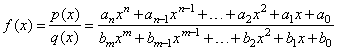 |
| where
n and m
define the degree of the numerator and the denominator
respectively. |
|
| Evaluating
the limit of a rational function at infinity |
| To
evaluate the limit of a rational function at infinity
we divide both the numerator and the denominator of
the function by the highest
power of x
of
the denominator. |
|
| Example: Evaluate
the limit |
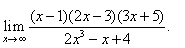 |
|
| Solution:
|
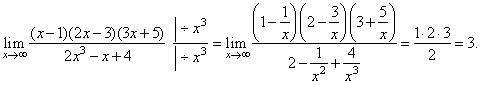 |
|
|
| Example: Evaluate
the limit |
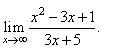 |
|
| Solution:
|
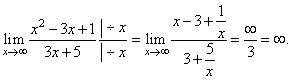 |
|
|
| Example: Evaluate
the limit |
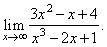 |
|
| Solution:
|
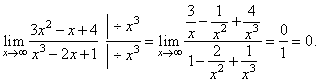 |
|
| Therefore,
the following three cases are possible; |
| 1.
If the degree of the numerator is greater than the degree of the
denominator (n
> m), then the
limit of the rational function does not exist, i.e., the
function diverges as x
approaches infinity. |
| 2.
If the degree of the numerator is equal to the degree of the
denominator (n
= m), then the limit of the rational function is
the ratio an/bm
of the leading coefficients. |
| 3.
If the degree of the numerator is less than the degree of
the denominator (n <
m), then the
limit of the rational function,
as x
tends to infinity, is zero. |
| The line
y
= c is a horizontal
asymptote of the graph of f(x)
if |
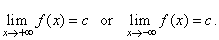 |
|
|
| Thus, a
rational function has a horizontal asymptote if the function
values tend to a constant value c as
x
approaches plus or minus infinity.
|