|
|
|
Symmetry
of a function, parity - odd and even functions
|
|
Transformations
of original or source function |
|
How
some changes of a function's notation affect the
graph of the function |
|
Translations
of the graph of a function
|
|
Reflections
of the graph of a function |
|
|
|
|
|
|
|
| Symmetry
of a function, parity - odd and even functions
|
| A
function ƒ
that changes neither sign nor absolute value when the sign of
the independent variable is changed is even,
so that, ƒ
(x)
= ƒ (-x). |
| Therefore,
the
graph of such a function is symmetrical with respect to the y-axis,
as is the graph shown in the left figure below. |
 |
 |
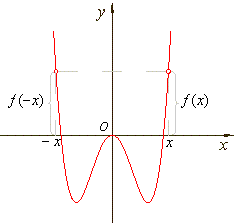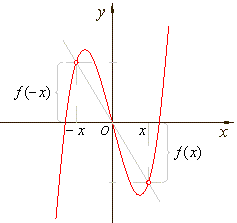| The
graph of an even function. |
The
graph of an odd function. |
|
| A
function ƒ
that changes sign but not absolute value when the sign of the
independent variable is changed is odd,
so that, ƒ
(x)
=
-
ƒ (-x).
That is,
for each x
in the
domain of ƒ,
ƒ (-x)
= -ƒ
(x).
|
| Therefore,
the
graph of such a function is symmetrical with respect to the
origin, as is the graph shown in the right figure above. |
|
| Transformations
of original or source function |
| How
some changes of a function notation affect the
graph of the function |
| Some
changes
in a function expression
(or an equation/formula)
do not affect the shape or the form of the
graph of the original
or the given function y
= ƒ (x). |
| Such
changes include use of geometrical transformations to the graph
of the function, like
translations (or shifts) of the graph of the
original function in
the direction of the coordinate axes, or its reflection across
the axes. |
|
| Translations
of the graph of a function
|
| The
graph of a translated function y
= ƒ (x - x0)
is
obtained translating (shifting) the graph of its
original or source function y
= ƒ (x)
horizontally by
x0
units to the right. |
| The
graph of a translated function y
= ƒ (x) +
y0
or y
- y0
= ƒ (x)
is obtained translating (shifting) the graph of its
original function y
= ƒ (x)
vertically by
y0
units up. |
| The
graph of a translated function y
= ƒ (x - x0)
+ y0 or
y
- y0
= ƒ (x - x0)
is
obtained translating (shifting) the graph of its
original function y
= ƒ (x)
in both directions of the coordinate axes, horizontally by
x0
units
to the right and vertically
by
y0
units up. |
|
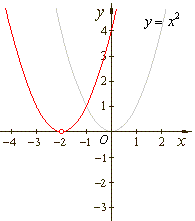
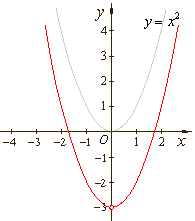
| Example: Draw
the graphs of the given three quadratic polynomials, |
| a)
y
= x2 + 4x + 4 = (x + 2)2,
b)
y
= x2 -
3
and
c)
y
= x2 + 4x + 1
or
y
+ 3 = (x + 2)2 |
| as
the translations of the same source quadratic y
= x2. |
 |
 |
 |
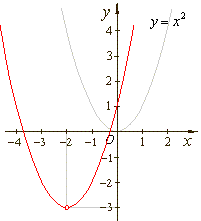| a)
y
= (x + 2)2 |
b)
y
= x2 -
3 |
c)
y
+ 3 = (x + 2)2 |
|
|
| Reflections
of the graph
of a function |
|
Change of the sign of
the independent variable of a function, denoted as y
= ƒ (-x),
reflects the graph of the given (original) function y
= ƒ (x)
across the y-axis. |
| Change
of the sign of the function, denoted
as y
= - ƒ
(x),
reflects the graph of the given function y
= ƒ (x)
across the x-axis. |
| Changes
of the signs of both, independent variable and the function, denoted as
y
= -
ƒ (- x),
reflect
the graph of the given function y
= ƒ (x), across the y-axis
and the x-axis. |
|
| Example: Given quadratic
polynomial y
= ƒ (x) = x2 + 4x + 1
or
y
+ 3 = (x + 2)2,
transform to: |
|
a) y
= ƒ (-
x),
b)
y
= -
ƒ (x)
and c) y
= - ƒ
(-
x),
and draw corresponding graphs. |
|
| Solution:
a)
y
= ƒ (- x)
= (-x)2 + 4(-x) + 1
= x2 - 4x + 1
or
y + 3 = (x
-
2)2 |
|
b) y
= -ƒ
(x)
= -
(x2 + 4x + 1)
= -
x2
-
4x - 1
or
y -
3 = -(x + 2)2 |
|
c) y
= -ƒ
(-x)
= -
((-x)2 + 4(-x) + 1)
= -
x2 +
4x - 1
or
y - 3 =
-
(x
-
2)2 |
 |
 |
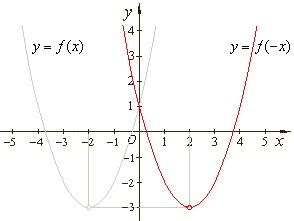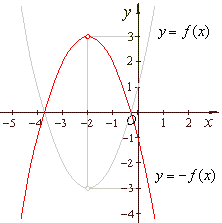| a)
y
+ 3 = (x - 2)2 |
b)
y
- 3 =
- (x + 2)2 |
|
 |
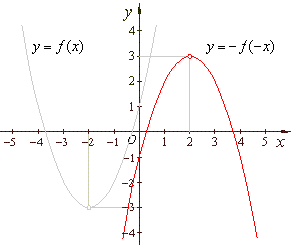| c)
y
= -
x2 + 4x
- 1
or
y
- 3 =
- (x
- 2)2 |
|
|
|
|
|
|
|
|
|
|
|
| Calculus
contents A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
