|
|
|
 The
instantaneous
rate of change or the derivative
The
instantaneous
rate of change or the derivative |
|
Continuity and discontinuity
of a function |
|
Vertical,
horizontal and oblique or slant asymptotes |
|
|
|
|
|
|
|
|
| The
instantaneous
rate of change or the derivative |
| Thus,
if the slope or gradient m
of the secant line passing through the points (x1,
ƒ(x1))
and (x2,
ƒ(x2))
of the graph of a function
is
positive, the function is increasing (going up), as shows the
figure below. |
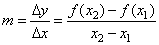 |
| where,
x2
-
x1>
0 |
| |
|
|
 |
|
| Since
the difference x2
-
x1 is
always positive, when the function is decreasing (going down), the slope will be negative. |
| The
ratio of the rise and the run, called the difference quotient,
that equals the value of the tangent of the angle between the
direction of the secant line and x-axis,
becomes the slope (gradient) of the tangent line as the difference Dx
tends to zero, and is called the instantaneous
rate of change or the derivative
at the point of the function. |
| For
a given function ƒ and point
(x1,
ƒ (x1)), the
derivative of ƒ at
x
= x1
is the slope of the tangent line through the point (x1,
ƒ
(x1)),
i.e., f
'(x1)
= tan
at
. |
| The
gradient of a curve at a point on its graph, expressed as
the slope of the tangent line at that point, represents the rate of
change of the value of the function and is called derivative of
the function at the point, written |
| y'
=
dy/dx
=
f
'(x) |
|
| Continuity and discontinuity |
| A
function that has no sudden changes in value as the variable
increases or decreases smoothly is called continuous function. |
| Or
more formally, a real function y
=
ƒ (x)
is continuous at a point a
if the limit of ƒ
(x)
as x
approaches a
is ƒ
(a). |
| If
a function does not satisfy this condition at a point it is said
to be discontinuous, or to have a discontinuity
at that point. |
|
| Vertical,
horizontal and oblique or slant asymptotes |
| A
line whose distance from a curve decreases to zero as the
distance from the origin increases without the limit is called
the asymptote. |
| The
definition actually requires that an asymptote be the tangent to
the curve at infinity. Thus, the asymptote is a line that the
curve approaches but does not cross. |
|
| Vertical
asymptote |
| The
line x =
a is a vertical asymptote
of a function ƒ
if ƒ
(x)
approaches infinity (or negative infinity)
as x
approaches
a
from the left or right. |
|
| Horizontal
asymptote |
| The
line y =
c is a horizontal
asymptote of a function ƒ
if ƒ
(x)
approaches c
as
x
approaches
infinity (or negative infinity). |
|
| Oblique or slant
asymptote |
| The
line y =
mx
+ c is a
slant or oblique asymptote of
a function ƒ
if ƒ
(x)
approaches
the line
as
x approaches infinity
(or negative infinity). |
|
-
- - -
- - - |
| The
functions that most likely have asymptotes are rational
functions. |
| So,
vertical asymptotes occur when the denominator of the simplified
rational function is equal to 0. Note that the simplified
rational function has cancelled all factors common to both the
numerator and denominator. |
|
| The
existence of the horizontal asymptote is related to the degrees
of both polynomials in the numerator and the denominator of
the given rational
function. |
| Horizontal
asymptotes occur when either, the degree of the numerator is
less then or equal to the degree of the denominator. |
In
the case when the
degree (n) of the numerator is less then the degree
(m) of the
denominator,
the x-axis
y =
0
is the asymptote. |
| If
the degrees of both polynomials, in the numerator and the denominator, are equal then,
y = an/bm
is the horizontal asymptote,
written as the ratio of their highest degree term coefficients respectively. |
| When
the degree of the numerator of a rational function is greater
than the degree of the denominator, the function has no
horizontal asymptote. |
|
| A
rational function will
have a slant (oblique) asymptote
if the
degree (n)
of the numerator is exactly one more than the degree (m)
of
the denominator that is if n
= m + 1. |
| Dividing
the two polynomials
that form a rational function,
of which the
degree
of the numerator
pn(x)
is exactly one more than the degree
of
the denominator qm
(x), then |
| pn
(x)
= Q (x) · qm(x) + R
=>
pn (x)/qm
(x)
= Q (x) + R/qm (x) |
| where,
Q (x)
=
ax + b
is the quotient and R/qm
(x)
is the remainder with constant R. |
| The
quotient Q
(x)
=
ax + b
represents the equation of the slant asymptote. |
| As
x
approaches
infinity (or negative infinity),
the remainder R/qm
(x)
vanishes (tends to zero). |
| Thus,
to find the equation of the slant asymptote, perform the long
division and discard the remainder. |
|
| The
graph of a rational function will never cross its vertical
asymptote, but may cross its
horizontal or slant asymptote. |
|
-
- - -
- - - |
| Example: Given
the rational function |
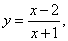 |
sketch
its graph. |
|
| Solution:
The
vertical asymptote can be found by finding the root of the
denominator, |
|
x + 1 = 0 =>
x = -1
is the vertical asymptote.
|
|
The
horizontal asymptote is the ratio of their
highest degree term coefficients since
the degree of polynomials in the numerator and denominator are equal,
|
| |
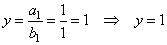 |
is the
horizontal asymptote. |
|
|
The graph of the given rational function is translated equilateral (or rectangular)
hyperbola shown below.
|
| The
rational function of the
form
|
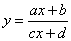 |
can
be rewritten into
|
|
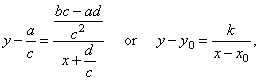 |
|
|
| where, x0
and y0
are asymptotes and k
is constant. |
|
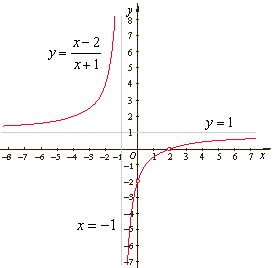 |
|
|
Therefore, values of the vertical and
the horizontal asymptote correspond to the coordinates of the horizontal and the vertical translation
of the source equilateral hyperbola y
= k/x, respectively.
|
|
|
| Example: Given
the rational function |
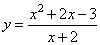 |
sketch
its graph. |
|
| Solution:
The
vertical asymptote can be found by finding the root of the
denominator, |
|
x + 2 = 0 =>
x = -2
is the vertical asymptote.
|
| Since
the
degree
of the numerator is exactly one more than the degree of
the denominator the given rational function has the slant
asymptote. |
| By dividing the
numerator by the denominator |
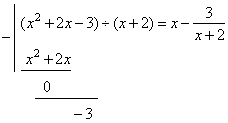 |
| obtained is
the slant asymptote y
= x |
| and
the
remainder
3/(x + 2) that vanishes as x
approaches
positive or negative infinity. |
|
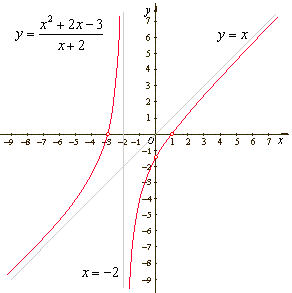 |
|
|
|
|
|
|
|
|
|
|
|
| Calculus
contents A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |