Integral calculus
      The indefinite integral
      Trigonometric integrals
        Trigonometric integrals of the form ∫ sinm x, cosn x dx
        Integrals of the rational functions containing sine and cosine,   ∫ R (sin x, cos x) dx
Trigonometric integrals
Trigonometric integrals of the form
∫ sinm x, cosn x dx
where m and  n are integers, we use the following substitutions;
  1)   if  m  is a positive odd integer then,  cos x = t
  2)   if  n  is a positive odd integer then,  sin x = t
  3)   if  m + n  is a negative even integer then,
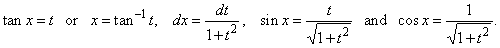
If  m and  n are positive even integers then the integrand expression can be transformed using the following
trigonometric identities,
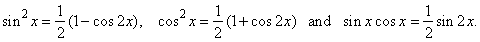
In the following examples use appropriate substitutions and trigonometric identities given above.
Example:  85. Evaluate
Solution: 
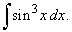Example:  86. Evaluate
Solution: 
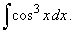Example:  87. Evaluate
Solution: 
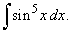Example:  88. Evaluate
Solution: 
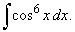Example:  89. Evaluate
Solution: 
Example:  90. Evaluate
Solution: 
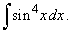This integral we can solve using the integration by parts formula, thus
Example:  91. Evaluate
Solution: 
Example:  92. Evaluate
Solution: 
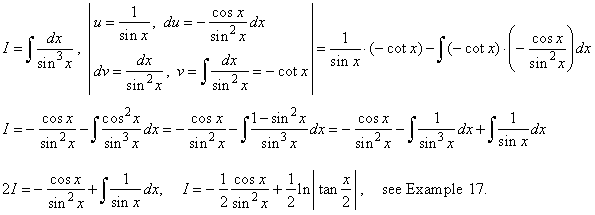
Calculus contents F
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.