|
| Integral
calculus |
|
|
|
The
indefinite integral |
Binomial
integral
|
|
Solving
binomial integrals examples
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Binomial
integral
|
|
Integral
of the form
|
|
|
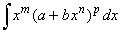
is
called the binomial integral where, a
and b
are real numbers while m,
n
and p
are rational numbers.
|
|
If
m,
n
and p
all are integers then the integrand is a rational function
integration of which is shown above.
|
|
There
are only three cases the binomial integral can be solved by
elementary functions:
|
|
1. if m
and n
are
fractions and p
is an integer then, the integral can be solved using
substitution x
= t s, where
s
is the least common denominator of m
and n.
|
|
|
|
2. if p
is a fraction
and (m +
1) / n is an
integer, then the integral can be solved using substitution
|
|
a + bxn = t s,
where s
is denominator of p.
|
|
3. if p
is a fraction
and (m +
1) / n + p
is an integer then, the integral can be solved using substitution
|
|
ax - n
+ b = t s,
where s
is denominator of p.
|
|
|
|
Solving
binomial integrals, examples
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Calculus contents
F |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
