|
| Integral
calculus |
|
|
The
indefinite integral |
 Substitution rule
Substitution rule |
|
Evaluating the indefinite integrals using substitution
rule examples
|
|
Evaluating the indefinite integrals using substitution
rule
solutions
|
|
|
|
|
|
|
|
| Substitution
rule |
| Let
f
and g
are differentiable, with range of g
contained in the domain of f,
and let F
be antiderivative of f such
that F'
(u)
= f (u) where u
= g (x), then |
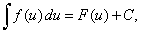 |
| by
applying the chain rule |
| F(g (x))' =
F' (g (x)) g' (x) = f
(g
(x)) g' (x) . |
| Thus,
obtained is substitution rule |
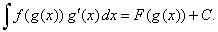 |
|
| Evaluating
indefinite integrals using substitution rule, examples
|
| Evaluate
the following indefinite integrals using substitution rule |
| 31. |
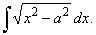 |
32. |
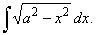 |
|
| 33. |
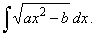 |
34. |
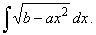 |
|
| 35. |
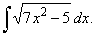 |
36. |
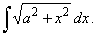 |
|
| 37. |
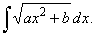 |
38. |
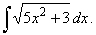 |
|
|
|
|
| Evaluating the indefinite integrals using substitution rule,
solutions
|
|
| Example:
31.
Evaluate |
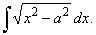 |
|
|
|
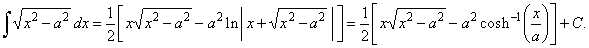 |
|
| Example:
32.
Evaluate |
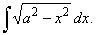 |
|
|
|
|
| Example:
33.
Evaluate |
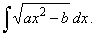 |
|
| Solution:
|
Let's show that given
integral is similar to that solved in the example 31. |
|
|
|
|
| Example:
34.
Evaluate |
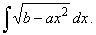 |
|
|
|
|
| Example:
35.
Evaluate |
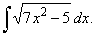 |
|
|
|
|
|
|
| Example:
36.
Evaluate |
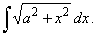 |
|
|
|
|
| Example:
37.
Evaluate |
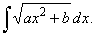 |
|
| Solution:
|
Let's show that given
integral is similar to that solved in the above example 36. |
|
|
|
|
| Example:
38. Evaluate |
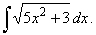 |
|
|
|
|