|
Graphs of rational
functions examples |
|
|
|
|
|
|
| The
graphs of the rational functions |
| ·
Rational
functions - a ratio of two polynomials |
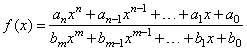 |
|
-
Reciprocal
function |
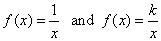 |
| |
-
Translation of the reciprocal function,
called linear rational function. |
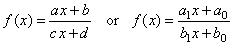 |
|
| The
functions that most likely have vertical, horizontal and/or
slant asymptotes are rational functions. |
|
| Vertical asymptotes of
rational functions |
| Vertical asymptotes occur when the
denominator of the simplified rational function is equal to 0.
Note that the simplified rational function has cancelled all
factors common to both the numerator and denominator. |
|
| Horizontal asymptotes
of rational functions |
| The
existence of the horizontal asymptote
is related to the degrees of both polynomials in the numerator
and the denominator of the given rational function. |
| Horizontal
asymptotes occur when either, the degree of the numerator is
less then or equal to the degree of the denominator. |
In
the case when the degree (n)
of the numerator is less then the degree (m)
of the denominator, the x-axis
y = 0
is the asymptote. |
| If
the degrees of both polynomials, in the numerator and the
denominator, are equal then, y
= an/bm
is the horizontal asymptote, written as the ratio of their
highest degree term coefficients respectively. |
| When
the degree of the numerator of a rational function is greater
than the degree of the denominator, the function has no
horizontal asymptote. |
|
| The oblique or slant
asymptote of rational functions |
| A
rational function will
have a slant (oblique) asymptote
if the
degree (n)
of the numerator is exactly one more than the degree (m)
of
the denominator that is if n
= m + 1. |
| Dividing
the two polynomials
that form a rational
function, of which the
degree
of
the numerator pn
(x)
is exactly
one more than the degree of the denominator qm
(x),
then |
| pn
(x)
= Q (x) · qm (x) + R
=>
pn (x)/qm (x) = Q(x)
+ R/qm (x) |
| where,
Q (x)
=
ax + b
is the quotient and R/qm
(x)
is the remainder with constant R. |
| The
quotient Q
(x)
=
ax + b
represents the equation of the slant asymptote. |
| As
x
approaches
infinity (or negative infinity),
the remainder R/qm
(x)
vanishes (tends to zero). |
| Thus,
to find the equation of the slant asymptote, perform the long
division and discard the remainder. |
| The
graph of a rational function will never cross its vertical
asymptote, but may cross its
horizontal or slant asymptote. |