|
Graphs of rational
functions examples |
|
|
|
|
|
|
| The
graphs of the rational functions |
| ·
Rational
functions - a ratio of two polynomials |
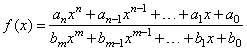 |
|
-
Reciprocal
function |
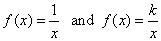 |
| |
-
Translation of the reciprocal function,
called linear rational function. |
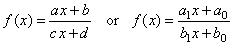 |
|
|
| The
graph of the reciprocal
function, equilateral or rectangular hyperbola |
| The
graph of the reciprocal function y =
1/x or y = k/x
is a rectangular (or
right) hyperbola of which asymptotes are the coordinate axes. |
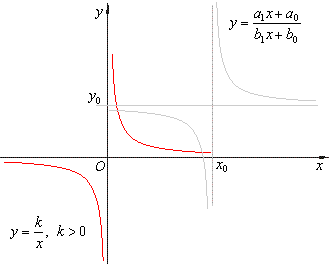
| If
k > 0
then, the function is decreasing from zero to negative infinity
and from positive infinity to zero, i.e., the graph of the
rectangular hyperbola opening in the first and third quadrants
as is shown in the right figure. |
| The
vertices, |
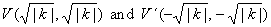 |
|
|
|
 |
|
|
|
Translation of the reciprocal function, linear rational
function |
| The
rational function |
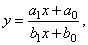 |
by
dividing the numerator by denominator, |
|
| can
be rewritten into |
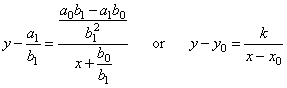 |
where, |
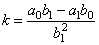 |
|
| is
the constant, |
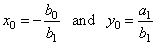 |
are
the vertical and the horizontal asymptote respectively. |
|
|
Therefore, the values of the vertical and the horizontal asymptotes
correspond to the coordinates of the horizontal and the
vertical translation of the reciprocal function y = k/x
as is shown in the figure
below.
|
 |
|