|
|
|
|
Higher order derivatives and higher order differentials |
 Higher order derivatives
Higher order derivatives |
|
Higher order derivatives examples |
|
|
|
|
|
|
|
Higher order derivatives |
| Higher
order derivatives are successive derivatives of the same function. Thus,
the second derivative is the derivative
of the first derivative, and the derivative of the second derivative is
third derivative and so on. |
| We
denote higher
order derivatives of the same function as follows, |
| the
second derivative is |
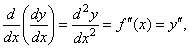 |
|
| the
third derivative is |
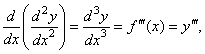 |
|
| and
the
nth
derivative is |
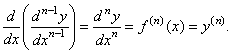 |
|
|
|
Higher order derivatives
examples |
|
Example:
Find
successive derivatives of y
=
xn
where n
Î
N.
|
|
Solution:
The
first derivative,
y'
= n x
n -1,
y''
=
n (n
-
1)
x
n -
2,
y'''
= n (n
-
1)(n
-
2)
x
n -
3, ...
|
| and
the
nth
derivative, y
(n)
= n (n
-
1)(n
-
2)
. . . [n
-
(n
-
1)]
= 1 · 2 · 3 ·
. . .
·
n
= n!,
y
(n)
= n!. |
|
|
Example:
Find
successive derivatives of y
= sin x.
|
|
Solution:
y'
= cos
x
=
sin (x
+ p/2),
y''
=
-
sin
x
=
sin [x
+ 2(p/2)],
|
|
y'''
=
-
cos
x
=
sin [ x
+ 3(p/2)],
y
(4)
= sin
x
=
sin [ x
+ 4(p/2)], ... |
|
and the
nth
derivative, y
(n)
=
sin [ x
+ n(p/2)]. |
|
|
Example:
Find
successive derivatives of
y
= cos x.
|
|
Solution:
y'
= -
sin
x = cos (x
+ p/2),
y''
=
-
cos
x = cos [x
+ 2(p/2)],
|
|
y'''
= sin
x = cos [x
+ 3(p/2)],
y
(4)
= cos
x = cos [x
+ 4(p/2)], ... |
|
and the
nth
derivative, y
(n)
= cos [x
+ n(p/2)]. |
|
|
Example:
Find
successive derivatives of
y
=
ex.
|
|
Solution:
The
first derivative,
y'
= ex,
y''
=
ex, ...
and
the
nth
derivative,
y
(n)
= ex.
|
|
|
Example:
Find
successive derivatives of
y
=
ax.
|
|
Solution:
y'
= ax
ln a,
y''
=
ax
ln2a,
y'''
=
ax
ln3a, ...
and
the
nth
derivative,
y
(n)
= ax
(ln a)n.
|
|
|
Example:
Find
successive derivatives of
y
=
ln
(1 + x).
|
|
Solution: |
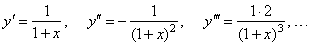 |
|
| and the
nth
derivative, |
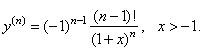 |
|
| |
|