|
|
|
|
The chain rule
applications |
Implicit differentiation |
|
Implicit differentiation examples |
|
Generalized power rule |
|
Generalized power rule examples |
|
|
|
|
|
| Implicit
differentiation |
| Let
given a function F
= [y (x)]n,
to
differentiate F
we use the power rule and the chain rule, |
 |
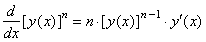| which,
for example, for n =
2 gives |
 |
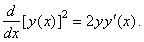| The
same method we use to differentiate an equation of a curve given in the
implicit form |
| F(x,
y) = c or F(x,
y) = 0. |
| So,
the chain rule applied to differentiate the above equation with respect
to x
gives |
|
|
| Meaning,
differentiate the equation with respect to both variables at the same
time such that, when differentiating
with respect to x,
consider y
constant,
while when differentiating
with respect to y,
consider x constant
and multiply by y'. |
|
|
Implicit differentiation examples |
|
Example:
Calculate
the derivative y' of the
equation of the curve x2
+ y2 -
2axy
= 0.
|
|
Solution:
We
use the above method of implicit differentiation to find
y'
of the
equation,
|
 |
|
|
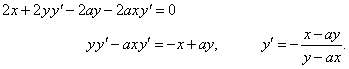Example:
Let
determine the equation of the line tangent to the ellipse b2x2
+ a2y2 = a2b2
with the center at the origin, at the point (x1,
y1).
|
|
Solution:
Differentiating
the equation of the ellipse we get,
|
 |
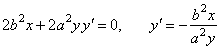| so
the slope |
 |
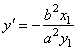of the line
tangent to the ellipse at the point (x1,
y1). |
|
| Therefore,
the equation of the line tangent to the ellipse
at the point (x1,
y1)
is |
 |
|
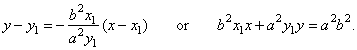| Generalized
power rule |
| If
given f (x)
= x r
where x >
0
and r
Î
R,
we can write f
(x)
= e r ln x
and apply the chain rule, then |
|
|
| For |
 |
 |
|
|
|
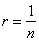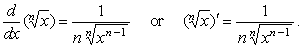| Example:
Find
the derivative of the function |
 |
|
|
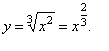| Solution: |
 |
|
|
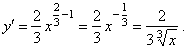| Example:
Find
the derivative of the function |
 |
|
|
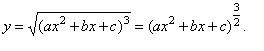| Solution: |
 |
|
|
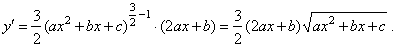| Example:
Find
the derivative of the function |
 |
|
|
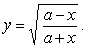| Solution: |
 |
|
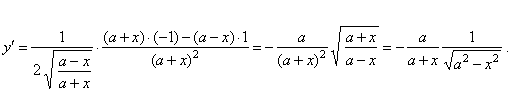