|
| Integral
calculus |
|
|
|
|
The
definite integral |
 Physical
applications to the definite integral
Physical
applications to the definite integral |
|
Describing
motion of objects using velocity - time graphs |
 Evaluating
the area under the graph of a function using the definition of the
definite integral, examples
Evaluating
the area under the graph of a function using the definition of the
definite integral, examples |
|
|
|
|
|
|
|
| Physical
applications to the definite integral |
| Describing
motion of objects using velocity - time graphs |
| In
kinematics motion is defined as change in position relative to some fixed point or
object. |
| The
distance the object travels in a period of time is its speed. Velocity
is speed in a given direction. |
| The
displacement is the vector form of the distance involving direction and
magnitude of the change in position of
the object, meaning it is the straight line distance between the initial
and final positions of the body. |
| Acceleration
is the increase in speed or velocity over a period of time. |
|
| Example:
When
an object travels with a constant velocity v
over a period of time t,
the displacement d,
for the object
we
calculate using the formula d
= v · t. |
| Then,
the
constant velocity v
is represented in the coordinate system (t,
v)
as
a line parallel to the t-axis
passing
through the point (0,
v)
while the displacement
d
is given by the area of the rectangle with the base t
and
height v,
as is shown in the left figure below. |
|
|
|
| Example:
If
an object travels with constant acceleration a
then its velocity v
is changing by a constant amount
each unit of time t. |
| Thus,
the velocity v
= a · t
is represented as the line through the origin with slope equal to the
acceleration, as
shows the velocity-time graph in the right picture above. |
| When
an object travels with constant acceleration a
then
displacement
d
traveled in a certain amount of time t
is the same as object travels with constant velocity v
= (a · t)/2, that
is, equals
the half of the final velocity at
the end of the time interval. |
| Therefore,
the length of the path an object travels with constant acceleration
in a given time interval is represented
in the velocity-time graph by the area of the rectangle of the base t
and height (at)/2 |
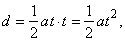 |
| that
correspond to the area of the triangle of the base t
with height at,
shown in the above figure. |
|
| Evaluating
the area under the graph of a function using the definition of the
definite integral, examples |
| Example:
Evaluate
the area under the graph of the quadratic function over the interval [0,
x],
where
x
is any value
of the argument, using the
definition of the definite integral. |
| Solution: Let's
use the partition of the interval [0,
x] into n
equal subintervals,
so that Dx
=
x /
n
and calculate the
lower sum s
of inscribed rectangles, as
is shown in the left figure below. According to
definition |
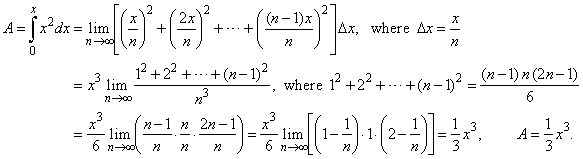 |
| The
area under the graph of
f(x) = x2
over the interval [0,
x] amounts 2/3
of the area of the triangle OPxP. |
|
|
|
| Example:
Evaluate
the area under the graph of the rectangular or equilateral hyperbola f
(x)
= 1/x over the interval [1,
x],
using the
definition of the definite integral. |
| Solution:
Let's divide the interval [1,
x]
into n
subintervals of different lengths by partition points that form |
| the
geometric sequence, 1,
q, q2, . . . , qn -
1, qn = x (q > 1) |
| and
calculate the lower and upper sums, s
and S,
as is shown in the right figure above. |