|
| Graphing
Linear Equation, Linear Function (First Degree Polynomial)
|
|
|
|
General
form of the equation of a line
|
|
The
two point form of the equation of a line
|
|
|
|
|
|
|
| General
form of the equation of a line
|
| The linear equation
Ax +
By +
C
= 0 in two unknowns, x
and y, of
which at least one of the coefficients, A
or B, are different then zero,
is called the general form for the equation of a line. |
| Dividing the
equation by
B, where
B
is not 0, gives |
| |
 |
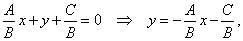where |
 |
|
|
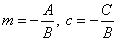| the slope-intercept form
y
= mx
+ c
of a line. |
| By putting
C
= 0 into the general form obtained is |
 |
|
|
|
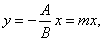the equation of the
line that passes through the origin. |
| Setting
A = 0, gives |
 |
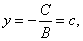the
line parallel to the x-axis. |
|
| Setting B = 0 gives |
 |
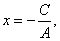the
line parallel to the y-axis. |
|
|
| The
two point form of the equation of a line
|
| Two points
P1(x1,
y1)
and P2(x2,
y2)
determine a unique line on the
Cartesian plane. |
| Therefore, their coordinates satisfy the equation
y
= mx
+ c
of the line. |
| The line which passes through the point
P1(x1,
y1) |
|
is determined by the equation y -
y1
= m(x
- x1). |
| As the
point P2(x2,
y2)
lies on the same line, |
| its coordinates should satisfy
the same equation
y2 -
y1
= m(x2
- x1). |
| That way determined is
the slope |
 |
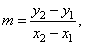where
x2
- x1
is not 0. |
|
|
|
| Thus, obtained is |
 |
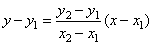the equation of the line passing through the two points. |
|
|
| Example:
Find the equation of the line which passes through points P(-2, 3) and
Q(6,
-1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents C |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
