|
| Quadrilaterals,
Polygons - Regular Polygons |
|
|
|
Cyclic quadrilateral |
|
Tangential quadrilateral
|
|
Polygons
|
|
Regular
polygons |
|
|
|
|
|
|
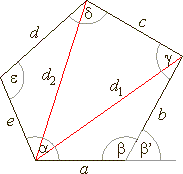
| Cyclic quadrilateral |
| A
quadrilateral inscribed in a circle, so that all its vertices
lie on the circumference is called a cyclic
quadrilateral. |
| The
opposite angles of a cyclic quadrilateral are supplementary. |
|
 |
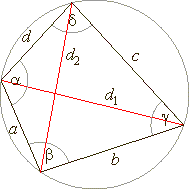| a
+ g = b + d = 180°, |
| d1
· d2
= a · c + b
· d |
| perimeter
P
= a + b
+ c
+ d, s
= 1/2P |
| area |
 |
|
|
|
|
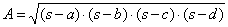| Tangential quadrilateral
|
| A
quadrilateral whose sides all lie tangent to the circle
inscribed within the quadrilateral is called a tangential
quadrilateral. |
|
 |
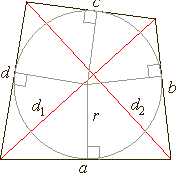| s
= a +
c = b + d, |
| perimeter
P
= a + b
+ c
+ d, s
= 1/2P |
 |
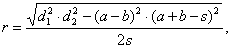| area |
A
= r · s |
|
|
|
|
| Polygons
|
| A
polygon is closed plane figure
bounded by a number of straight line segments with the same
number of vertices. |
| The
sum of interior angles is (n
-
2) · 180°, where n
is the number of sides of a polygon. |
| The
sum of exterior angles of a polygon is 360°. |
|
 |
| dn
- number
of diagonals |
| b'
- the
exterior angle |
| dn
= 1/2 · n · (n
-
-
3) |
|
| Sn=
(n
-
2)
· 180° |
- the
sum of interior angles |
|
|
|
| Regular
polygons |
| In
a regular polygon all sides are equal and all its angles are
equal. |
| The
exterior angle of a regular polygon is b'
= 360°/n, where n
is the number of sides of a regular polygon. . |
|
 |
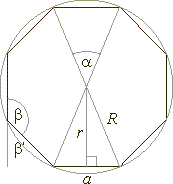| a
=
b'
= 360°/n
|
b'
- the
exterior angle |
| b
=
180°
-
b'
= (n
-
2)
· 180°/n, |
P = n · a |
| dn
= 1/2 · n · (n
-
-
3) |
- number
of diagonals |
| A
= 1/2 · n · a · r
= 1/2P · r |
-
area of a regular polygon |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents D |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
