|
| Coordinate Geometry or
Analytic Geometry |
|
|
|
|
Plane Analytic Geometry |
Coordinate
plane, points, line segments and lines
|
|
The distance formula
|
|
The midpoint formula
|
|
Dividing
a line segment in a given ratio |
|
Area
of a triangle |
|
The
coordinates of the centroid of a triangle |
|
|
|
|
|
| Coordinate
plane, points, line segments and lines
|
| The distance formula
|
| The
distance between two given points in a coordinate
(Cartesian) plane. |
|
|
| The midpoint formula
|
| The
point on a line segment that is equidistant from its endpoints
is called the midpoint. |
|
|
|
| Dividing a line segment in a given ratio
|
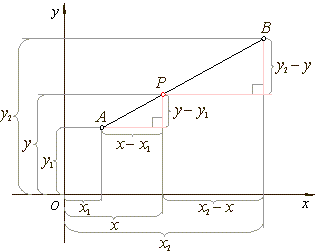
| A
given line segment AB
in a Cartesian plane can be divided by a point P
in a fixed ratio, internally or externally. |
| If
P
lies between endpoints then it divides AB
internally. If P
lies beyond the endpoints A
and B
it divides the segment AB
externally. |
| The
ratio of the directed lengths l
=
AP
:
BP |
| is
negative in the case of the internal division since the segments
AP
and BP
have opposite sense, while in the external division, the ratio l
is positive. |
 |
|
| As
l
=
AP
:
BP |
| and
shown triangles are similar, then |
 |
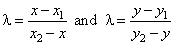| which,
with l
negative, gives |
|
|
| the coordinates of
the point P. |
| |
|
|
|
| Area
of a triangle |
| The
rectangular coordinates of three points in a coordinate plane
describe a triangle. Using given coordinates we derive the
formula for the area of the triangle, as is shown in the diagram
below. |
 |
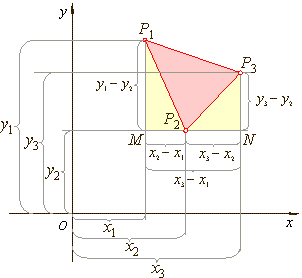| The
area of the given triangle P1P2P3
equals |
| the
area of the trapezium P1MNP3
minus
the |
| sum
of the areas of the right triangles, P1MP2
and |
| P2NP3,
that is |
| PD =
1/2·[(y1 -
y2)
+ (y3 -
y2)]
· (x3 -
x1)
- |
| -
1/2·[(y1
- y2)·(x2
- x1)
+ (y3 -
y2)·(x3
- x2)] |
| which
after simplifying and rearranging gives |
| PD=1/2·[x1(y2
- y3)
+ x2(y3 -
y1)
+ x3(y1 -
y2)] |
|
|
|
| The
coordinates of the centroid of a triangle |
| The
point of coincidence of the medians of a triangle is called the
centroid. |
|
The
median is a straight line joining one vertex of a triangle to
the midpoint of the opposite side and divides the triangle into
two equal areas.
|
| The
centroid cuts every median in the ratio 2
: 1 from a vertex to the
midpoint of the opposite side. |
| The
coordinates of the centroid of a triangle given its three
points, P1, P2 and
P3
in a coordinate plane: |
| The
centroid M(x,
y),
where |
x
= 1/3 · (x1 + x2
+ x3), y =
1/3 · (y1
+ y2
+ y3) |
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents E |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved |
