|
| Boolean
Algebra |
|
|
|
Binary
addition |
|
The
half adder |
|
The
Binary
addition circuit - the full adder |
|
|
|
|
|
|
|
|
| Binary
addition |
| The
binary system works under the same principles as the decimal
system as show basic rules for binary addition: |
| (1) |
|
|
|
0 |
+ |
0 |
= |
|
0 |
|
|
| (2) |
|
|
|
0 |
+ |
1 |
= |
|
1 |
| (3) |
|
|
|
1 |
+ |
0 |
= |
|
1 |
| (4) |
|
|
|
1 |
+ |
1 |
= |
1 |
0 |
(with a carry of
1) |
| (5) |
|
1 |
+ |
1 |
+ |
1 |
= |
1 |
1 |
(with a carry of
1) |
|
or |
| (1) |
(2)
and (3) |
(4) |
(5) |
|
|
|
1 |
|
0 |
1 |
1 |
1 |
| + 0 |
+
0 |
+
1 |
+
1 |
|
0 |
1 |
10 |
11 |
|
|
|
|
|
1 |
1 |
carry |
|
|
1 |
1 |
0 |
1 |
0 |
|
=> |
26 |
|
+ |
1 |
1 |
1 |
0 |
0 |
|
=> |
+ 28 |
|
1 |
1 |
0 |
1 |
1 |
0 |
sum |
54 |
|
When adding two multiple digits numbers a carry
has to be added to the
next higher place value digit.
Thus,
in order to design a logical circuit that
performs a binary addition we should form a truth table with two
columns for binary inputs, a
and b,
and columns
for the outputs, the sum (S) and carry (c). |
|
|
|
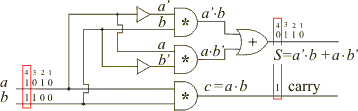
| The
half adder |
| |
a |
b |
a´ |
b´ |
a´· b |
a ·
b´ |
carry |
Sum |
| 1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
| 2 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
| 3 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
| 4 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
 |
|
|
The above circuit is named a
half adder because it only register a carry as the result of addition of the two binary 1's from the
input (marked with 4).
The circuit which is capable to perform
the addition of three bits (as the column marked with 6 in the right example), i.e., that includes a carry from a previous column, is called a
full adder and is shown below. |
|
|
| |
|
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
| |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
| |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
a
= 54 |
| |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
b
= 45 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
+ c
(carry) |
| |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
S = 99 |
|
|
|
| The
Binary
addition circuit - the full adder |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
