|
|
|
|
Integral
calculus
|
|
|
|
The area between the graph
of a function and the x-axis over a closed interval
|
|
Geometric
interpretation of the definite integral
|
|
Until
now we assume that the integrand, the function that is integrated, to be
nonnegative or f (x)
>
0
for all x
in an interval [a,
b]. |
|
Now suppose f
(x)
<
0
in
the whole interval or in some of its parts then, the areas of regions
between the graph
of f
and the x-axis,
which lie below or above the x-axis,
differ in the sign of f
(x). |
|
|
| Therefore,
the definite integral yields the algebraic sum of these areas taking
regions below the x-axis
negative,
as show the figures above. |
| So,
if the graph of f
looks
as in the left figure above then |
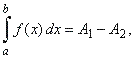 |
|
| hence
the definite integral represents the algebraic sum of the areas above
and below the x-axis. |
| Thus,
as the right figure above shows, follows that |
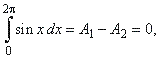 |
|
|
as the area A2,
lying under the arc of the sinusoid in the interval [p,
2p]
is congruent to the area A1
in [0,
p]
but with opposite sign. |
|
|
Properties
of the definite integral
|
| 1)
The definite integral
over interval of zero length |
|
Since
the definite integral we evaluate as the limit of Riemann sums, the
basic properties of limits hold for integrals
as well. Thus, the limit of Riemann sums show the first property |
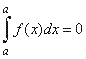 |
| as
the upper limit b
tends to lower limit a,
written b
®
a. |
| 2)
Reverse
order of integration |
|
By
reversing the upper and lower limits of integration to b
< a, that is, passing
through the x-axis
from a
to b in
opposite direction, each difference, x1
-
a, x2 -
x1, . . . , b -
xn
- 1
of Riemann sums becomes negative
while function values, f
(xi')
can stay unchanged, therefore
|
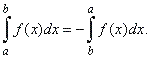 |
| The definite integral
changes sign if the limits of integration interchange. |
| 3)
The constant multiple rule |
|
Suppose
f
(x)
is integrable over the
interval [a,
b] and c
is any real number, then c
f
(x)
is integrable over [a,
b] such that |
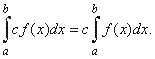 |
| If
integrand is multiplied by a constant, we can factor out the constant. |
| 4)
The integral of the sum or difference of two functions |
| Suppose
f
(x)
and g
(x)
are integrable over the
interval [a,
b] then |
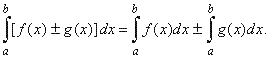 |
| The
integral of the sum or difference of two functions is the sum or
difference of the integrals of each function. |
| 5)
Internal addition of the definite integral |
|
Suppose
f
(x)
is integrable over the
interval [a,
b] and c
is a point inside the interval, i.e., a
< c < b then, the
additive
property of the definite integral holds
|
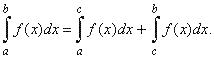 |
|
Let
for example c
lies outside the interval such that c
< a < b, and
assume f
(x)
is integrable over the
interval [c,
b] then,
|
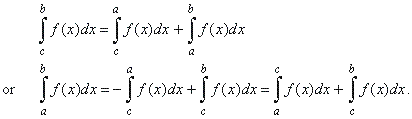 |
| Therefore,
the above rule holds for any arrangement of three points, a,
b
and c. |
| 6)
The definite integral of an odd function |
|
If
the integrand is an odd function f
(x) = -
f
(-x),
the graph of which is symmetrical about the origin, with the
interval of integration [-
a,
a],
then
|
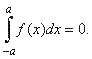 |
| 7)
The definite integral of an even function |
|
If
the integrand is an even function f
(x) = -
f
(x), the graph of
which is symmetrical about the y-axis,
with the
interval of integration [-
a,
a],
then
|
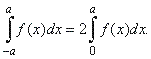 |
| 8)
The definite integral of a nonnegative and
non-positive functions |
| Suppose
f
(x)
is integrable over the
interval [a,
b] and f
(x) >
0 but not identically
equal to zero, then |
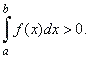 |
| If
f
(x)
is integrable over the
interval [a,
b] and f
(x) <
0 but not identically
equal to zero, then |
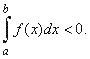 |
| 9)
Relationship of the definite integrals of two functions over the same
interval of integration |
| Suppose
f
(x) and g
(x) are integrable over the
interval [a,
b] and f
(x) >
g
(x) for all x
in [a,
b], then |
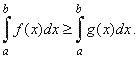 |
| 10)
Absolute integrability |
| Suppose
f
is integrable over the
interval [a,
b], it can be shown
that | f
(x)| is also
integrable on [a,
b] |
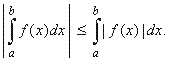 |
| Since,
-
|
f
(x)| <
f
(x) <
|
f
(x)|, then |
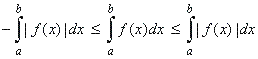 |
| what
means the same as the above. |
| 11)
The mean value theorem |
|
Suppose f
(x)
is integrable over the
interval [a,
b] and m
and M
are minimal and maximal value of the function,
that is m
<
f
(x) <
M
for all x
in [a,
b], then |
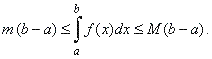 |
|
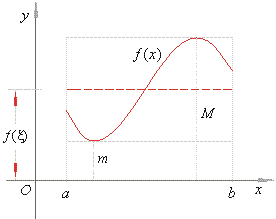
Geometric
meaning of the above inequality is that the area under the graph of f
(x) over the
interval [a,
b] is contained inside
the rectangles with the same base (b
-
a)
and of the heights m
and M. |
|
Since f
(x)
is continuous in the
interval [a,
b] it takes at least
one time each value between m
and M
inside the interval. |
|
Therefore, there is at least one
value x
inside the
interval [a,
b] such that |
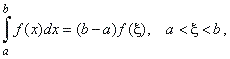 |
|
meaning, there
exists the rectangle with the base
(b
-
a)
and a height f
(x)
whose area equals the
|
|
 |
|
|
area under the graph of f
(x) over the
interval [a,
b]. |
| 12)
The average value of a function over the given interval |
|
For
a continuous function f
over an
interval [a,
b], the average value
of f
(x) is defined as
|
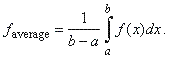 |
|
Thus,
the average value of a function f
(x) over an
interval [a,
b] is equal to some
value of the function between
its minimal and maximal value inside the interval, as shows the above
figure.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents
L
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|