|
|
Vectors in a Plane and Space |
|
|
Vector
product or cross product |
 Vector
product
Vector
product |
|
Right-handed system |
|
An example for the vector product in physics |
|
The condition for two vectors to be parallel |
|
The vector products of the standard unit vectors |
|
The vector product properties |
|
The vector product in
the component form |
 The
vector product and the mixed product use, examples
The
vector product and the mixed product use, examples |
|
|
|
|
|
|
|
| Vector
product or cross product |
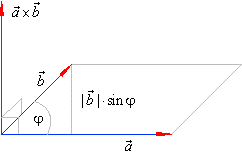
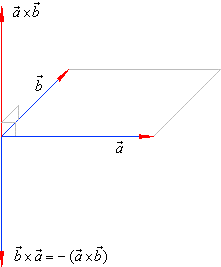
| The vector product of two vectors,
a
and b
is the vector
a ´
b
perpendicular to given vectors, and the
magnitude of which |
| |
a ´
b
|
= | a | · | b | · sinj,
where j is the angle between
a
and b. |
That is, the vector product
a ´
b
is the vector magnitude
of which equals the area of a parallelogram with sides a
and b, and the direction
of which is perpendicular to the plane of the given vectors, forming a
right-handed system as is shown in the below diagram, |
|
|
|
A right-handed system is so called because
vectors,
|
|
a ,
b
and a
´
b have
the orientation of the thumb, the
|
|
forefinger, and the middle finger of the right
hand.
|
|
That is, if the thumb is placed in the
direction of the first operand (a)
and the forefinger in the direction of the second operand
(b), then the resultant vector
(a
´
b)
is coming out of the middle finger.
|
|
 |
|
|
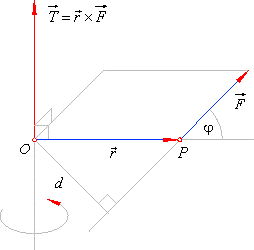
| An example for the vector product in physics |
| An example for the vector product in physics is
a torque (a moment of a force - a rotational force). |
|
The force applied to a lever, multiplied by its distance from the lever's fulcrum
O,
is the torque
T, as
is shown in the diagram.
|
|
r = OP is the vector from the axis of rotation to the point
P
on which the force is acting.
|
|
The distance from the direction
line of the force to O
is,
|
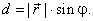
|
|
If a force of magnitude |
F | acts at an angle
j to the
displacement arm, and within the plane perpendicular to the
rotation axis, then from the definition of the cross product,
the magnitude of the torque is,
|
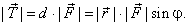
|
The direction of the torque is determined by the vector
product,
|
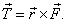
|
|
 |
|
|
|
The vector product is not commutative,
that is
|
|
|
|
The thumb of the right hand is now placed in the direction of
b,
the forefinger in the direction of
a, and thus the middle
finger points in the direction of b
´
a.
|
|
Two non-zero vectors are parallel
if
|
|
|
|
that is, the angle between
vectors (a,
b)
= 0°
or 180°.
|
The vector product of a vector with itself or with a parallel
vector is zero or the null vector, i.e.,
|
|
|
|
 |
|
|
| The vector products of the standard unit vectors |
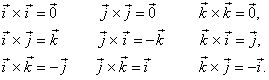 |
|
 |
|
|
| The vector product properties: |
|
|
|
|
|
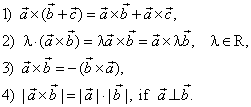 |
|
|
| The vector
product in the component form |
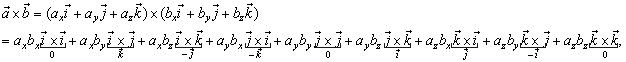 |
|
|
| -
the vector or cross product in the component form. |
| The
above component notation of the vector product can also be written formally as a symbolic determinant expanded by minors
through the elements of the first row. A minor is the reduced determinant formed by omitting the
i-th row and
j-th column of a matrix, multiplied by
(-1)i
+ j. |
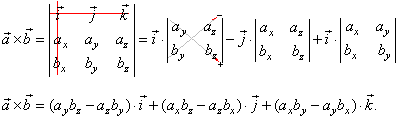 |
|
| The vector product
and the mixed product use examples |
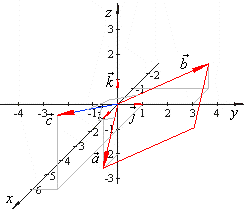
| Example:
Given are vectors, a
= i -
2 k and
b =
-
i + 3 j + k,
determine the vector
c
= a
´
b
and the area of a parallelogram formed by vectors, a
and b.
|
| Solution: |
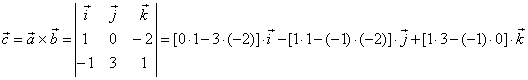 |
|
|
|
| The
area of the parallelogram, |
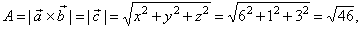 |
| or |
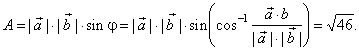 |
|
|
 |
|
|
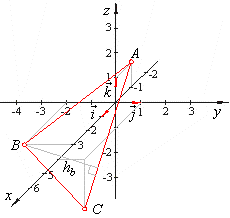
| Example:
Vertices of a triangle are, A(-1,
0, 1), B(3,
-2,
0) and C(4,
1, -2),
find the length of the altitude hb.
|
|
Solution:
Using
the area of a triangle,
|
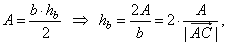 |
| as
the area of the triangle
|
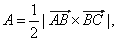 |
where |
|
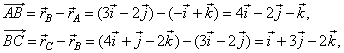 |
|
 |
|
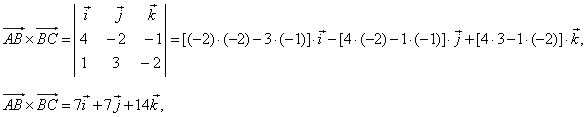 |
| then,
the area of the triangle, |
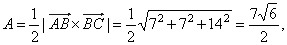 |
|
|
| and the
length of the side b, |
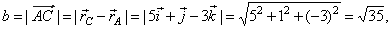 |
|
|
|
| thus,
the length of the altitude, |
|
|
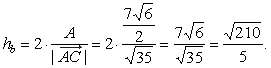 |
|
|
|
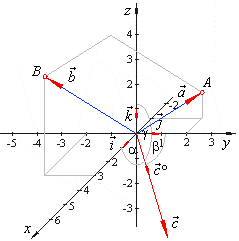
| Example: Find
the angles that the unit vector, which is orthogonal to the plane formed
by vectors,
|
| a
= -i +
2 j + k
and b
= 3i -
2
j + 4k,
makes with the coordinate axes. |
|
Solution:
The
unit vector which is orthogonal to the plane, formed by
the vectors, a
and b,
is the direction vector of a vector c,
such that
|
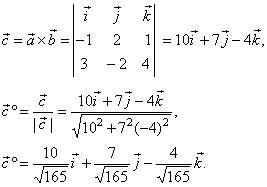 |
|
 |
|
| Angles,
which the unit vector
c°
forms with coordinate axes, we find by using the formula, |
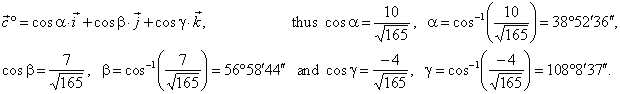 |
|
| Example: Given
are vectors,
a
= -2i -
3 j,
b
= -i -
2
j + 3k
and c
= -i +
2
j + k,
find the projection
(the scalar component) of the vector a
onto vector d
= b ´
c.
|
| Solution:
Let first find
the vector d, |
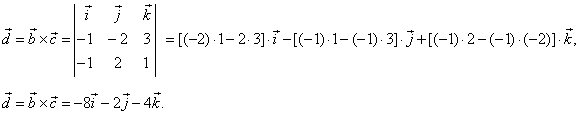 |
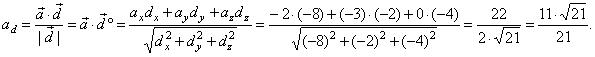 |
|