|
|
Vectors in a Plane and Space |
|
 Vectors
and a coordinate system, Cartesian vectors
Vectors
and a coordinate system, Cartesian vectors |
 Projection of a vector in the direction of another vector,
the scalar and vector components
Projection of a vector in the direction of another vector,
the scalar and vector components |
|
The scalar
component |
|
The vector component |
 Scalar product of vectors examples
Scalar product of vectors examples |
|
|
|
|
|
|
|
|
| Projection of a vector in the direction of another vector,
the scalar and vector components |
| The scalar
component |
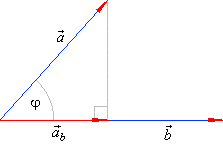
| The length of projection of
a
in the direction of
b
or the scalar component ab,
from the diagram, |
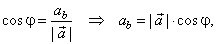 |
|
|
|
 |
|
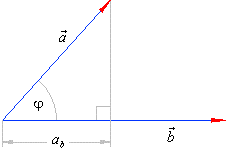
| Thus, the scalar component of a vector
a
in the direction of a vector b
equals the scalar product of the vector
a
and the unit vector b0
of the vector
b.
|
|
| The vector component |
| By multiplying the scalar component
ab, of a vector
a in the direction of
b, by the unit vector
b0
of the vector
b, obtained
is the
vector component
of a
in the direction of
b. |
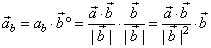 |
| or |
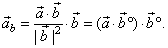 |
|
|
|
 |
|
|
| Scalar
product of vectors examples |
| Example:
Applying the scalar product, prove
Thales’ theorem which states that an angle inscribed in a |
| semicircle is a right angle. |
| Solution:
According to diagram in
the right figure |
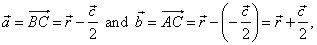 |
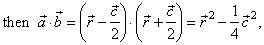 |
| since square of a vector equal to square of its length, |
|
 |
|
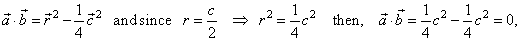 |
| thus,
a
and b are orthogonal vectors as |
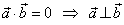 |
. |
|
|
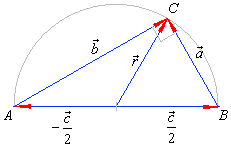
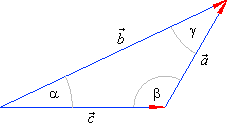
| Example:
Prove the law of cosines used in the trigonometry of oblique triangles. |
| Solution:
Assuming the directions of vectors as in
the right diagram |
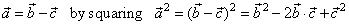 |
Using the scalar product and substituting square of vectors
by square of their lengths, obtained is |
| a2 =
b2 + c2 -
2bc · cosa
- the law of cosines. |
|
 |
|
| In the same
way, |
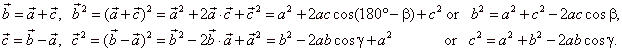 |
|
| Example:
Determine a parameter l so the given vectors,
a
= -2i
+ l
j
-
4k
and b
= i -
6 j + 3k
to be perpendicular. |
| Solution:
Two vectors are perpendicular if their scalar product is zero, therefore |
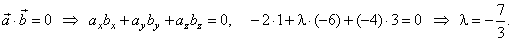 |
|
| Example:
Find the scalar product of vectors, a
= -3m
+ n
and b
= 2m -
4n if
| m |
= 3 and
| n |
= 5 , and the
angle between vectors, m
and n is
60°. |
|
|
|
| Example:
Given are vertices, A(-2,
0, 5), B(-3, -3,
2), C(1,
-2,
0) and
D(2,
1, 3), of a parallelogram, |
| find the
angle subtended by its diagonals as is shown in the diagram below. |
| Solution:
|
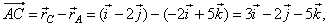 |
|
|
|
|
|
|
| Example:
Given are points, A(-2,
-3,
1), B(3, -1,
-4), C(0,
2, -1) and
D(-3,
0, 2), determine the scalar and
vector components of the vector AC
onto vector BD. |
| Solution:
The scalar component of the vector
AC
onto vector BD, |
|
|
|
The vector component of the vector
AC
in the direction of the vector BD
equals the product of the scalar component ACBD
and the unit vector BD°
that is
|
|
|
|
|
|
|
|
|
|
|
|
|
| Vectors
in 2D and 3D Contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |