|
| Unit vector |
| A vector
|
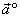 |
is called the
unit vector of a vector
|
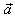 |
if
|
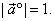 |
|
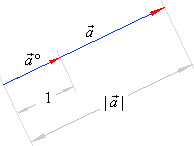
| Therefore,
|
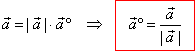 |
|
| the unit vector
|
 |
determines the direction of the vector
|
 |
|
|
 |
|
|
| Addition subtraction
and scalar multiplication of vectors examples |
| Example: |
Given are vectors,
|
 |
determine
|
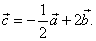 |
|
|
|
|
|
| Example:
Given is a regular hexagon
ABCDEF with the center
O. Express vectors
CD,
BE,
EA,
and CE,
in terms of vectors, AB
= a
and BC
= b.
|
| Solution:
|
|
|
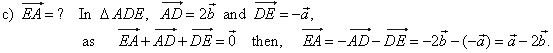 |
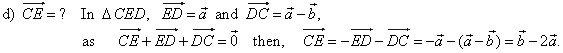 |
|
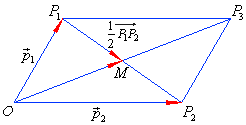
| Example: Determine the distance of the midpoint
M, of the segment
P1P2, and the point
O, if points,
P1
and P2
are heads of vectors p1
and p2 respectively, and whose tails coincide
with the point O
as shows the figure. |
| Solution: The
vector P1P2
represents the difference p2
-
p1. |
|
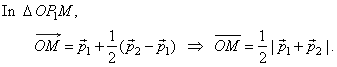 |
|
 |
|
|
| Example: In a triangle
ABC drown are medians as vectors,
|
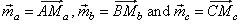 |
|
| Prove
that
|
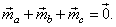 |
|
| Solution:
Replacing the sides of the triangle by vectors directed as in
the diagram,
|
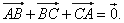 |
|
|
|
|
| Example:
Use vectors to prove that line segments joining the midpoints of adjacent sides of a quadrangle,
|
| form a parallelogram.
|
| Solution: The sides of the quadrangle ABCD are replaced by vectors, directed as in
the diagram so that the opposite vectors connecting midpoints are, |
|
|
| As equal vectors are of same lengths and parallel, therefore the line segments connecting the midpoints of any quadrangle, form a parallelogram. |
|
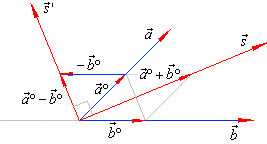
| Example:
Determine a vector which coincides with the angle bisectors of vectors, a
and b
in the diagram.
|
| Solution: The unit vectors of the vectors
a
and b
are,
|
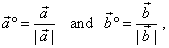 |
| and they form a rhombus whose diagonal is |
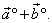 |
|
| That is, a vector |
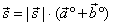 |
will coincide
with |
|
| the angle bisector, while a vector |
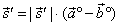 |
|
|
 |
|
| defines
the angle bisector of the supplementary angle of the angle between vectors, a
and b.
|
|
| Linear combination of
vectors |
| A vector
d
= l
a
+ m
b,
l, m
Î R
denotes the linear combination of the vectors, shown in the
left diagram. |
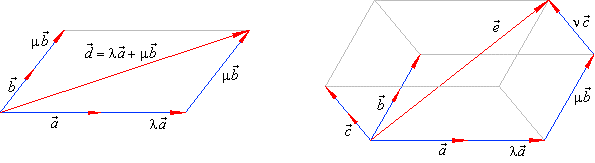 |
| On the same way, the vector
e
= l
a
+ m
b
+ n
c
represents the linear combination of the vectors,
a,
b
and c,
as shows the right diagram in the above figure. |
|
| Example:
Given is a parallelogram ABCD, the midpoint
M
of the side AD
and the intersection point O
of
|
| the diagonals. Express vectors,
AO,
BD,
and BM
as the linear combination of vectors,
a
= AB
and
|
| b
= AD.
|
|
|
|
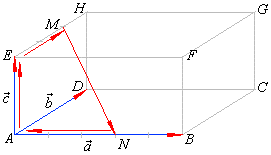
| Example:
To a cuboid ABCDEFGH the point
M
divides the edge EH
in the ratio EM
: MH
= 2 : 1 and
|
| the
point N
the edge AB
in the ratio AN
: NB
= 3 : 2. Express the vector
MN
as the linear combination of
|
| vectors,
a
= AB, b
= AD
and c
= AE.
|
|
|
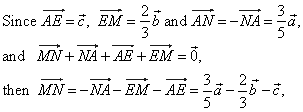 |
| MN
is the linear
combination
of the vectors, a,
b
and c. |
|
|
 |
|
|
| Linear dependence of
vectors |
| Vectors,
a
= OA
and b
= OB
whose points,
O, A and
B
all lie on the same line are said to be linear
dependent, but if the points,
O, A and
B
do not all lie on the same line then a
and b, are not collinear, and are said to be
linear independent. |
|
a)
If a
and b
are linear independent vectors then every vector
d
of the plane determined by
a
and b, can be
written as the linear combination of these vectors, that is in the form |
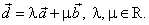 |
| Vectors,
a
= OA,
b
= OB and
c
= OC,
whose points,
O, A,
B
and C
all lie on the same plane, are said to be coplanar or linear dependent.
But if points, O, A,
B and
C
do not all lie on the same plane, then a,
b
and c
are not coplanar, and are said to be linear independent. |
b) If,
a,
b
and c are linear independent vectors in 3D space then every vector
d, from the space, can be
represented as |
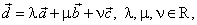 |
| that is, as the linear combination of the vectors,
a,
b
and c. |
| Thus, in the
last example the sides of the cuboid are replaced by three linear independent vectors,
a,
b
and c
so that the vector MN
can be written as the linear combination of the vectors, a,
b
and c. |