The graph of the tangent function f (x) = tan x, Properties of the tangent function, Zeros of the tangent function, Behavior of the tangent function

Trigonometry

Graphs of Trigonometric Functions

The Graph of the Tangent Function f (x) = tan x

Properties of the tangent function

Domain and range

Zeros of the tangent function

Parity and periodicity of the tangent function

The tangent function behavior and monotony

Graphs of trigonometric functions

The graph of the tangent function f (x) = tan x

By associating the ordinates of the points that according to definition equals the tangent of an arc in the unit circle, to corresponding arc x in a coordinate system obtained are points P (x, tan x) of the graph of the tangent function.

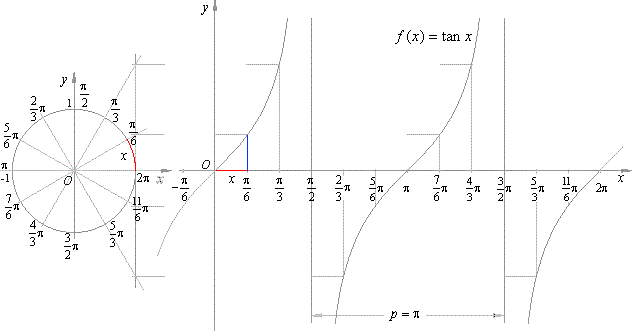Properties of the tangent function

- Domain and range

From the definition of the tangent, tan x = sin x/cos x, follows that all real numbers belong to the domain of the tangent function except the zeroes of the cosine function, thus

D_f = R \ {(2k + 1) · p/2, k Î Z}.

As shows the graph in the above figure, tangent function takes all real values from - oo to + oo as its argument x passes through an interval of the length p, therefore the range

f (D) = R or - oo < tan x < + oo.

- Zeros of the tangent function

The zeroes of the tangent are determined by the zeroes of the sine function in the numerator, so

x = kp, k Î Z.

- Parity and periodicity

The tangent is odd function since

f (-x) = tan (-x) = - tan x = - f (x).

It is obvious from the graph that the tangent is periodic function with the period p = p. Thus, for every arc x from the domain

tan (x + kp) = tan x.

Behavior of the tangent function (monotonicity - a function consistently increasing or decreasing in value)

The tangent is increasing function in every interval between any of the two successive vertical asymptotes

that is, f (x₁) < f (x₂) for all x₁ < x₂.

The equations of the vertical asymptotes are, x = p/2 + kp.

Trigonometry contents A