|
| Trigonometry |
|
Sum to product and
product to sum formulas or identities |
|
Sum to product formulas
for the sine and the cosine functions |
|
The product to sum
formulas for the sine and cosine functions |
|
Trigonometric identities,
examples |
|
|
|
|
|
|
|
| Sum to product and
product to sum formulas or identities |
| Sum to product formulas
for the sine and the cosine functions |
|
Adding the sum and difference formulas for the sine function,
|
| sin (a
+ b)
= sin a
· cos b
+ cosa
· sin b
(1) |
| sin (a
-
b)
= sin a
· cos b
-
cosa
· sin b
(2) |
| yields |
sin (a
+ b)
+
sin (a
-
b)
= 2sin a
· cos b |
|
|
| and
by subtracting the second from the first identity, |
|
sin (a
+ b)
-
sin (a
-
b)
= 2cosa
· sin b. |
| Then,
substitute a
+ b
= x and a
-
b
= y . |
| By
adding and subtracting these equalities we get |
 |
|
|
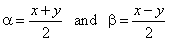| thus, |
 |
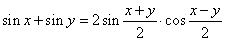and |
 |
|
|
|
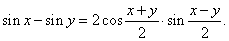| Using the same procedure for the cosine function, |
| cos
(a
+ b)
= cos a
· cos b
-
sin a
· sin b
(1) |
| cos
(a
-
b)
= cos a
· cos b
+ sin a
· sin b
(2) |
|
| by
adding (1)
+
(2) we get,
cos
(a
+ b)
+ cos
(a
-
b)
= 2cos a
· cos b |
| and subtracting
(1)
-
(2)
cos
(a
+ b)
-
cos
(a
-
b)
= -2sin
a
· sin b |
|
substitute, a
+ b
= x and a
-
b
= y
so that, |
|
|
|
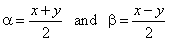| thus, |
 |
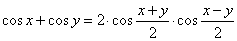and |
 |
|
|
|
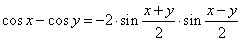| The product to sum
formulas for the sine and cosine functions |
| By adding and subtracting addition formulas derived are following product
to sum formulas, |
| |
 |
and |
 |
|
|
| |
 |
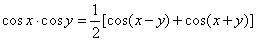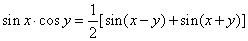and |
 |
|
|
|
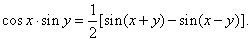| Trigonometric
identities
examples |
| Example:
Using known values, sin
60°
= Ö3/2
and sin 45°
= Ö2/2
evaluate sin 105°.
|
| Solution: Applying the sum formula for the sine function,
sin (a
+ b)
= sin a
· cos b
+ cosa
· sin b, |
| therefore,
sin 105°
= sin (60°
+ 45°)
= sin 60° · cos 45° + cos60°
· sin 45° |
 |
|
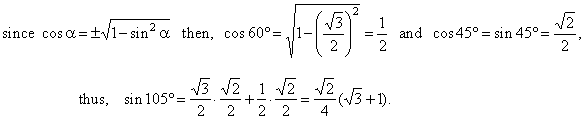| Example:
Prove the identity |
 |
|
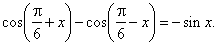| Solution:
Using the addition formula |
 |
|
 |
|
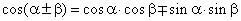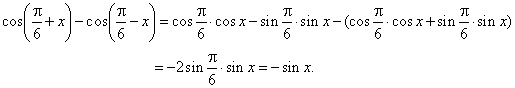| Example:
Verify the identity |
 |
|
|
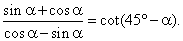Solution:
We divide the numerator and
denominator on the left side by sin
a
and to the right side we use the cotangent formula for the
difference of two angles, thus
|
 |
 |
|
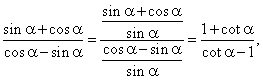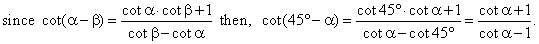| Example:
Express sin
3x in terms of sin
x. |
| Solution:
Using the sum formula and the double angle formula for the sine function, |
| sin
3x
= sin (2x + x)
= sin 2x · cos x + cos 2x · sin x
= 2sin x cos x · cos x + (cos2 x
-
sin2 x) · sin x |
|
= 2sin x · (1 -
sin2 x) + (1 -
2sin2 x) · sin x = 3sin x -
4sin3 x. |
|
| Example:
Prove the identity |
 |
|
|
|
|
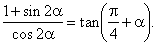| Example:
Prove the identity |
 |
|
|
|
|
|
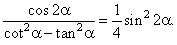Example:
Express the given
difference sin
61° -
sin 59° as a product.
|
| Solution:
Since |
 |
|
 |
|
|
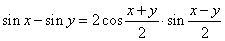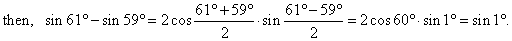Example:
Prove the identity sin a
+ sin (a
+ 120°) +
sin (a
+ 240°)
= 0.
|
|
Solution:
Applying the sum formula to
the last two terms on the left side of the identity we get,
|
 |
|
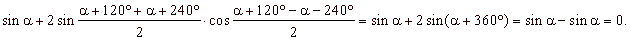| Example:
Prove that |
 |
|
|
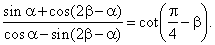Solution: Replace
sin a
by cos (p/2
-
a)
and cos a
by sin (p/2
-
a)
and use the sum to product
formula
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
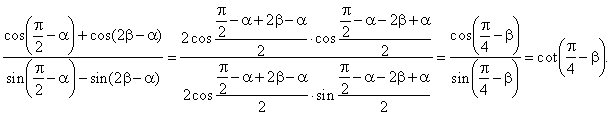| Trigonometry
contents A |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
