|
| Trigonometry |
|
The
addition formulas and related identities |
|
The sum and difference formulas
for the trigonometric functions |
|
Deriving the addition formulas
for sine and cosine functions |
|
The
addition formulas for tangent and cotangent functions |
|
|
|
|
|
|
|
|
The
addition formulas and related identities
|
|
The sum and difference formulas
for the trigonometric functions
- Trigonometric functions of the sum or difference of two angles in terms of separate functions of the angles.
|
|
Deriving the addition formulas
for sine and cosine functions
|
|
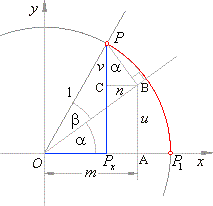
The coordinates of the terminal point
P(cos
(a
+ b),
sin (a
+ b)) |
|
of the arc a
+ b
on the unit circle shown on the right figure, we |
| can
write as |
| sin
(a
+ b)
= PxP = u + v
(1) |
| cos
(a
+ b)
= OPx = m -
n (2) |
| From
the right triangles, OBP,
CBP
and
OAB
it follows that, |
| in
DOBP,
OB
= cos b
and BP
= sin b |
|
 |
|
|
|
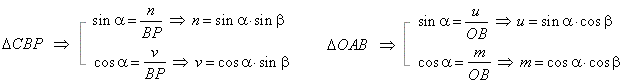
after substituting the obtained values
for, u,
v,
m
and n
into (1) and (2)
|
| |
sin (a
+ b)
= sin a
· cos b
+ cosa
· sin b |
|
|
| |
cos
(a
+ b)
= cos a
· cos b
-
sin a
· sin b |
|
|
|
By replacing b
with -b in the above
identities, we get
|
|
sin [a
+ (-b)]
= sin a
· cos (-b)
+ cosa
· sin (-b)
and since cos
(-b)
= cos b
|
|
cos [a
+ (-b)]
= cos a
· cos (-b)
-
sin a
· sin (-b)
and sin
(-b)
= -
sin b
|
|
|
| therefore, |
sin (a
-
b)
= sin a
· cos b
-
cosa
· sin b |
|
|
| |
cos
(a
-
b)
= cos a
· cos b
+ sin a
· sin b |
|
|
|
|
|
The
addition formulas for
tangent and cotangent functions
|
|
The addition formulas for the tangent and cotangent functions we derive from the
definitions, thus
|
|
|
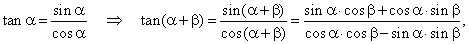
and by dividing the numerator and denominator by
cos a
· cos b,
|
|
|
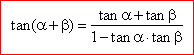
Using the relation
|
|
|
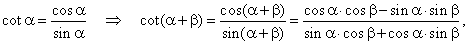
and after dividing the numerator and denominator by
sin a
· sin b,
|
|
|
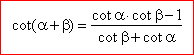
By replacing b
with -b in the above
identities, and substituting
|
|
tan
(-b)
= -
tan b
and cot
(-b)
= -
cot b,
we get
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Trigonometry
contents A |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
