|
| Trigonometry |
|
Basic relationships
between trigonometric functions of the same angle |
|
Basic
relationships between trigonometric functions of the same angle
shown in the unit circle |
|
Basic relationships
between trigonometric functions of the same angle shown in the
tabular form |
|
Basic relationships
between trigonometric functions of the same angle, examples |
|
|
|
|
|
|
|
|
|
|
Basic relationships
between trigonometric functions of the same angle shown in the
unit circle
|
|
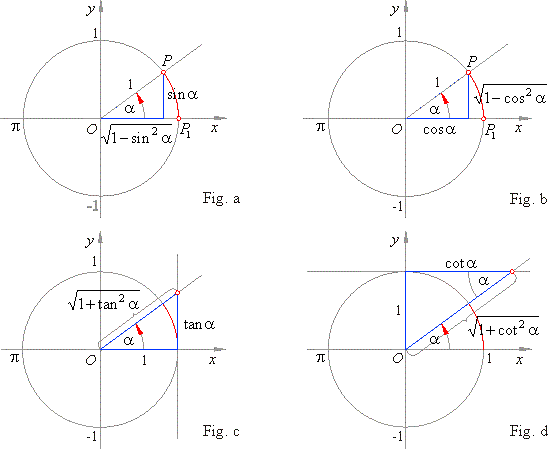
Given relations between the trigonometric functions of the same angle, expressed by absolute value,
are included in the definitions of the functions in right triangles shown in
Fig. a - d, and included in the table below.
|
|
|
|
|
Basic relationships
between trigonometric functions shown in the tabular form
|
|
|
|
|
Basic relationships
between trigonometric functions of the same angle, examples
|
| Example:
Find values of other trigonometric functions of
an angle a,
if given sin a
= -
4/5 and
|
|
270° < a
< 360°.
|
|
Solution:
Since a
is a forth-quadrant angle, then
|
|
|
|
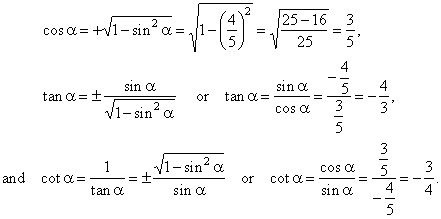
| Example:
Find the value
of |
 |
|
|
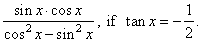Solution:
Dividing the numerator and
the denominator by
cos2 x,
|
|
|
|
| Example:
Prove the
identity |
 |
|
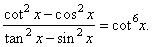| Solution: |
 |
|
|
|
|
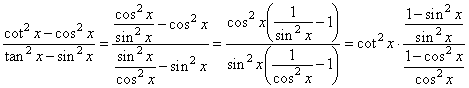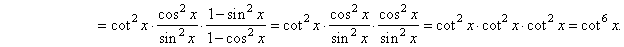
| Example:
Given
sin x + cos x
= a, find
sin4
x
+ cos4
x
.
|
|
Solution:
Since sin2
x
+ cos2 x = 1 then,
|
|
(sin2
x
+ cos2 x)2 = sin4
x
+ cos4 + 2sin2
x · cos2 x
= 1 or
sin4
x
+ cos4 = 1
-
2sin2
xcos2 x.
|
|
As given sin
x + cos x = a then,
(sin x + cos x)2 =
a2
or sin2
x
+ cos2 x
+ 2sin
x cos x = a2
|
|
therefore, sin
x
· cos x =
(a2
-
1)/2 and
it follows that sin4
x
+ cos4 = 1
- (a2
-
1)2/2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Trigonometry
contents A |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
