|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
|
 Fractions
Fractions |
| Proper and improper fractions,
mixed numbers |
|
| 39. |
Convert given
mixed number to improper fraction.
|
|
| Solution: |
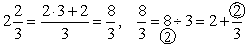 |
 |
|
| To
convert a mixed number to an improper fraction, multiply the
whole number by the denominator of the fraction, add the
numerator of the fraction to the product and write the sum over
the given denominator. |
| To
convert an improper fraction to a mixed number divide the
fraction's numerator by its denominator. The integer part of the
division is the integer part of the mixed number. The remainder
of the division is the numerator of the resulting fraction, as
is shown in the above example. |
|
| Converting and reducing fractions |
|
| 40. |
Write
equivalent fraction and reduce given fraction.
|
|
| Solution: |
Equivalent
fractions, |
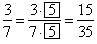 |
and |
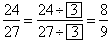 |
|
| Fractions that represent the same number are called equivalent fractions. |
|
For any fraction, multiplying the numerator and
denominator by the same nonzero number gives an
|
|
equivalent fraction.
|
| A fraction is in lowest terms when the greatest common factor of its numerator and denominator is 1. |
| To reduce a fraction to lowest terms, divide the numerator and denominator by their
greatest common factor. |
|
|
| Comparing fractions |
|
| 41. |
Compare
given fractions.
|
|
| To
compare fractions with different denominators, e.g. 4/5 and
7/9, multiply the numerator and the denominator of both fractions, the first fraction by the
denominator of the second fraction and the second fraction by the
denominator of the first fraction. We get equivalent fractions with the same
denominators, thus |
|
|
| To compare fractions with the same denominator, look at their numerators. The larger fraction is the one with the larger numerator. |
| If the numerators of two fractions are the same, the fraction with the
smaller denominator is the larger fraction. |
|
|
Decimal fractions
|
|
| 42. |
Given decimal fraction write as a vulgar fraction.
|
|
| Solution: |
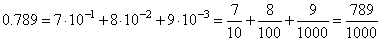 |
|
| Decimal
fractions are vulgar fractions whose denominator is a power of
ten. Or, it is a fraction written in the place-value notation with base 10
preceded by dot, after which
each successive digit indicates a multiple of the successive
negative powers of 10. |
|
|
| Adding and subtracting like
fractions |
|
| 43. |
Add and subtract given fractions.
|
|
| Solutions: |
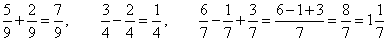 |
|
| To add or subtract two fractions with
the same denominator, add or subtract the numerators and write the sum over the common denominator. |
|
|
| Adding and subtracting fractions |
|
| 44. |
Add and subtract given fractions.
|
|
| Solutions: |
a) |
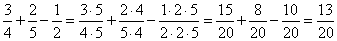 |
|
| |
b) |
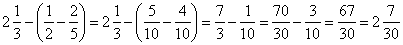 |
|
| To add or subtract fractions with different denominators: |
|
First find
the least common denominator (the smallest number that can be divided by each denominator). Write equivalent fractions using this
denominator. Then add or subtract the fractions.
|
|
| Multiplying fractions |
|
| 45. |
Multiply given fractions.
|
|
| Solution: |
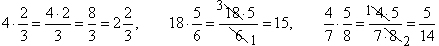 |
|
|
To multiply a whole number by a fraction means to
multiply it by a numerator and to divide a product by a denominator.
|
| When two fractions are
multiplied, the result is a fraction with a numerator that is the product of the fractions' numerators and
a denominator that is the product of the fractions' denominators. |
|
|
| Dividing
fractions, reciprocal fractions |
|
| 46. |
Divide given fractions.
|
|
| Solutions: |
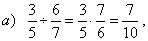 |
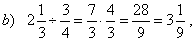 |
|
|
|
| To divide a number by a fraction, multiply the number by the
reciprocal of the fraction. |
| To divide mixed numbers, you should
always convert them to improper fractions, then multiply the first number by the reciprocal of the second. |
| To divide a fraction by a
whole number, write the whole number as an improper fraction with a denominator of 1, then multiply as fractions. |
|
| Simplifying complex fractions |
|
|
| 47. |
Simplify given complex fractions.
|
|
| Solutions: |
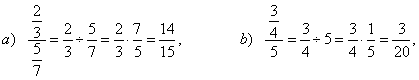 |
|
|
|
| Complex
fractions or compound fractions are fractions in which the
numerator and/or denominator contain fractions. |
| To simplify complex fractions, change the complex fraction into a division problem, i.e., divide the numerator by the denominator. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |