|
|
Vectors in a Plane and Space |
|
Vectors
and a coordinate system, Cartesian vectors |
|
Scalar product or dot
product or inner product |
|
Orthogonality or
perpendicularity of two vectors |
|
Different positions of two vectors and the corresponding values of
the scalar product |
|
Vectors examples |
|
|
|
|
|
|
|
| Scalar product or dot
product or inner product |
| On the beginning of this
section we have already mentioned that there are physical quantities as; force,
velocity, acceleration, electric and magnetic field and so on, which all have vectors’ properties. |
There’s another group of physical quantities as; distance, time, speed, energy, work, mass and so on, which
have magnitude but no direction, called scalar quantities or scalars. |
| The word scalar derives from the English
word "scale" for a system of ordered marks at fixed intervals used in measurement, which in turn is derived
from Latin scalae - stairs. |
| The magnitude of any vector is a scalar. |
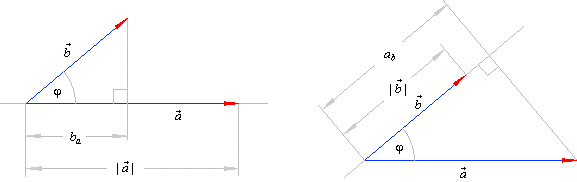
| The
scalar (numeric) product of two vectors geometrically is the product of the length of the first vector
with projection of the second vector onto the first, and vice versa, that is |
|
|
 |
 |
|
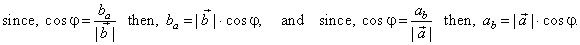| The scalar or the dot product of two vectors returns as the result scalar quantity as all three factors on the
right side of the formula are scalars (real numbers). |
| The result will be positive or negative depending on
whether is the angle j between the two vectors are acute or obtuse. |
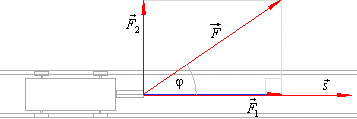
| For example, in physics mechanical work
W is the dot product of force
F and displacement
s, |
|
|
| Obviously, a change of the angle between the two vectors
changes the value of the work W, from the maximal value |
| for
j
= 0°
=>
W
= | F | ·
|
s |,
|
| to the minimal value |
| for
j
= 180°
=>
W
= - |
F | ·
|
s |. |
|
 |
|
| For j
= 90° the force
F
does any work on an object, since
|
 |
|
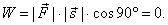| It is only the component of
the force along the direction of motion of the object which does any
work. |
|
| Orthogonality or
perpendicularity of two vectors |
| Therefore, if the scalar product of two vectors,
a
and b
is zero, i.e., a ·
b
= 0 then the two vectors are orthogonal. |
| And inversely, if two vectors are perpendicular, their scalar product is zero. |
|
|
|
| Different positions of two vectors and the corresponding values of
the scalar product |
| Different positions of two vectors and the corresponding values of their scalar product are shown in
the below figures. |
|
|
 |
|
|
|
 |
|
| Vectors
examples |
| Example:
Determine a parameter l so the given vectors,
a
= -2i
+ l
j
-
4k
and b
= i -
6 j + 3k
to be perpendicular. |
| Solution:
Two vectors are perpendicular if their scalar product is zero, therefore |
 |
|
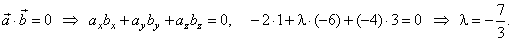| Example:
Find the scalar product of vectors, a
= -3m
+ n
and b
= 2m -
4n if
| m |
= 3 and
| n |
= 5 , and the
angle between vectors, m
and n is
60°. |
|
|
|
| Example:
Given are vertices, A(-2,
0, 5), B(-3, -3,
2), C(1,
-2,
0) and
D(2,
1, 3), of a parallelogram, |
| find the
angle subtended by its diagonals as is shown in the diagram below. |
| Solution:
|
 |
|
|
|
|
|
|
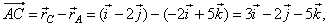| Example:
Given are points, A(-2,
-3,
1), B(3,
-1,
-4), C(0,
2, -1) and
D(-3,
0, 2), determine the scalar and
vector components of the vector AC
onto vector BD. |
| Solution:
The scalar component of the vector
AC
onto vector BD, |
|
|
|
The vector component of the vector
AC
in the direction of the vector BD
equals the product of the scalar component ACBD
and the unit vector BD°
that is
|
|
|
