|
| Trigonometry |
|
|
|
|
|
Trigonometric
Functions |
 Signs of trigonometric
functions
Signs of trigonometric
functions |
|
The table of signs of trigonometric
functions |
|
|
|
|
|
|
|
|
Signs of trigonometric
functions
|
|
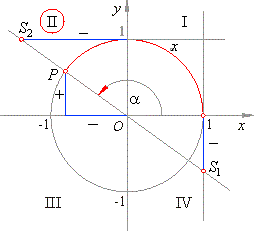
Quadrant I
- Values of trigonometric functions, sine, cosine, tangent and cotangent of any arc from
the first quadrant are all positive as positive are the coordinates of the points,
P,
S1
and S2
that define their values.
|
|
|
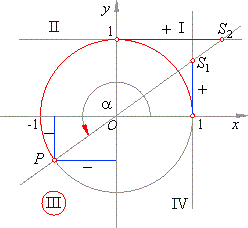
Quadrant II
- For arcs from the second quadrant points, P
and S2
both have negative abscissas (see the above figure), so the cosine and cotangent are negative. The ordinate of the terminal point
P
is positive so that the sine is positive while the ordinate of the point
S1
is negative, thus the tangent is negative.
|
|
|
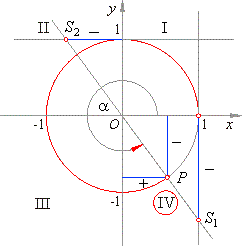
Quadrant III
- As the abscissas and the ordinates of the terminal points P
of arcs from the third quadrant (see the above figure) are negative it follows that cosine and sine functions of these arcs are negative. The ordinates
of the points
S1 and the abscissas of the points
S2 that belong to the arcs from the third quadrant are positive. Thus, the tangent and cotangent of these arcs are positive.
|
|
|
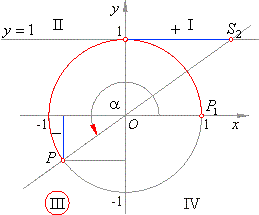
Quadrant IV
- The functions, sine, tangent and cotangent of the arcs from the fourth quadrant are negative as are the coordinates of the points,
P,
S1
and S2, that belong to them. Only the cosine function of arcs from the fourth quadrant is positive as are the abscissas of points
P that belong to them
(see the above figure).
|
|
|
|
The table of signs of trigonometric
functions
|

|
|
|
| Example:
To which quadrant belongs the endpoint of an arc
a
if
sin a < 0 and
cot a
> 0.
|
|
Solution: The
right figure shows that the ordinate of |
| the endpoint P
of an arc from the third quadrant is |
| negative, so sin
a < 0
while the abscissa of the
|
| point (in which the extension of the terminal side of |
| the angle
a
intersects the tangent y =
1) is positive, |
| i.e., cot
a
> 0.
|
| That is in accordance with the signs in the above
|
| table.
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus
contents C |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|