|
|
|
The coordinates of translations formulas |
|
The values of the
coefficients, a2
and a1
of the source quartic function y
= a4x4 + a2x2
+ a1x |
Graphing
the quartic polynomial function example |
|
|
|
|
|
|
|
| The
coordinates of translations formulas and the values of the
coefficients of the source quartic function |
| Thus,
y
= a4x4
+ a3x3
+
a2x2
+
a1x + a0
or y
-
y0
=
a4(x
-
x0)4
+
a2(x
-
x0)2
+
a1(x
-
x0), |
 |
 |
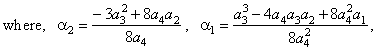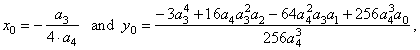| by
setting x0
=
0 and y0
= 0 we get
the source quartic y
=
a4x4
+
a2x2
+
a1x. |
|
|
|
| Graphing
the quartic polynomial function example |
| Example:
Given is quartic function
y
=
x4 -
4x3
+
4x2
+
x -
4,
find its source or original function and calculate the coordinates of translations, the zero
points, the turning points and the points of inflection. |
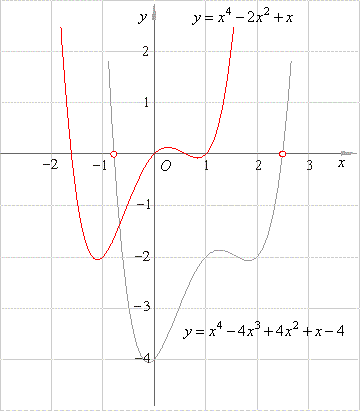
| Draw
graphs of the source and the given quartic function. |
| Solution:
1)
Calculate the coordinates of translations
|
 |
|
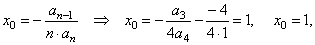y0
= f
(x0)
=> y0
= f (1)
= 14
-
4 · 13
+
4 · 12
+
1
-
4 =
-
2,
y0
= -
2 |
| 2)
To
get the source quartic, plug the coordinates
of translations into the general
form
of the quartic function, |
| y
+ y0
=
a4(x
+
x0)4
+
a3(x
+
x0)3
+ a2(x
+
x0)2
+ a1(x
+
x0)
+ a0 thus, |
| y
-
2
= (x
+
1)4
-
4(x
+
1)3
+
4(x
+
1)2
+ (x
+
1) -
4
so, y
=
x4
-
2x2
+
x
is
the source function. |
| Since
the coefficients of the source quartic function y
=
a4x4 +
a2x2
+
a1x
satisfy the conditions, |
 |
|
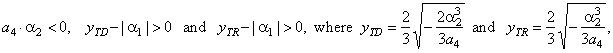the given quartic is the type 4/6 whose source graph has four
zeroes, three turning points and two points of inflection. |
| The
zeroes of the source quartic
y
=
x4
-
2x2
+
x
are, |
. |
|
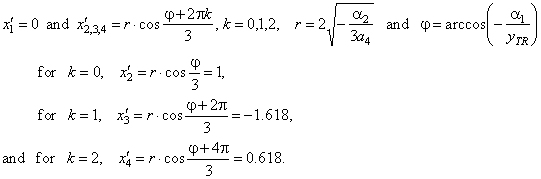The abscissas of the turning points
of the given quartic y
=
x4 -
4x3
+
4x2
+
x -
4,
|
|
|
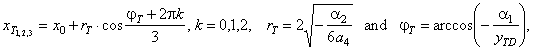
xT1
=
1.837, xT2
=
-
0.107 and xT3
=
1.269. |
| The points of
inflection of the given quartic, |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
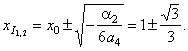| Pre-calculus contents
E |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
