|
|
|
The coordinates of translations formulas |
|
The values of the
coefficients, a2
and a1
of the source quartic function y
= a4x4 + a2x2
+ a1x |
The
basic classification criteria diagram |
|
The graphs of quartic functions
and their characteristic points |
|
The quartic
type 1, y
-
y0 = a4(x -
x0)4,
a2
= 0 and a1
= 0 |
|
The quartic type 2,
y
-
y0 = a4(x -
x0)4 + a1(x
-
x0),
a2
= 0 |
|
|
|
|
|
|
|
| The
coordinates of translations formulas and the values of the
coefficients of the source quartic function |
| Thus,
y
= a4x4
+ a3x3
+
a2x2
+
a1x + a0
or y
-
y0
=
a4(x
-
x0)4
+
a2(x
-
x0)2
+
a1(x
-
x0), |
 |
 |
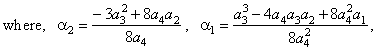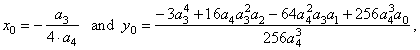| by
setting x0
=
0 and y0
= 0 we get
the source quartic y
=
a4x4
+
a2x2
+
a1x. |
|
|
|
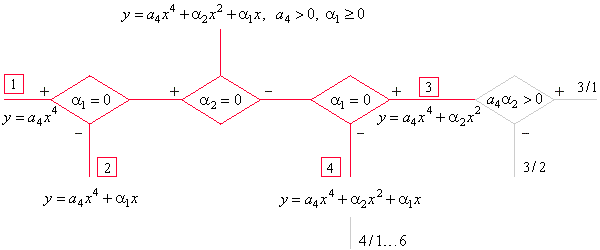
| The
basic classification criteria diagram for the quartic function |
| By
setting the coefficients a2
and a1
of the source quartic to zero, interchangeably, obtained is the
basic classification shown in the diagram. |
 |
|
| The
graphs of quartic functions and their characteristic points |
| There are
ten types (different shapes of the graphs) of quartic functions |
| type
1 |
y
= a4x4
+ a3x3
+
a2x2
+
a1x + a0
or y
-
y0
=
a4(x
-
x0)4,
a2
= 0 and a1
=
0. |
|
 |
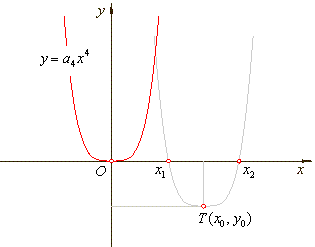| The
zeroes or roots: |
 |
|
|
|
|
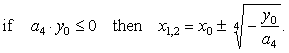| type
2 |
y
= a4x4
+ a3x3
+
a2x2
+
a1x + a0
or y
-
y0
=
a4(x
-
x0)4
+ a1(x
-
x0),
a2
= 0. |
|
 |
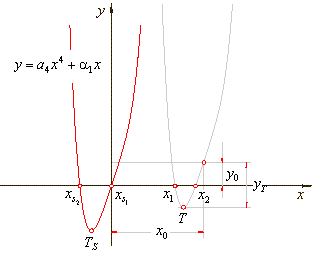| The
zeroes of the source function: |
 |
 |
|
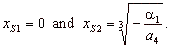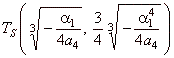| The
zeroes of the translated function we get
by adding x0
to the solution of the
equation a4x4
+ a1x +
y0
= 0. |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
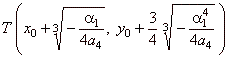| Pre-calculus contents
E |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
