|
|
|
|
Parametric Equations |
The parametric equations of a
quadratic
polynomial,
parabola |
|
The
parametric equations of the parabola, whose axis of symmetry is parallel
to the y-axis
|
|
The parametric equations of the
parabola, whose axis of symmetry is
parallel to the x-axis |
|
|
|
|
|
|
| The parametric equations of a
quadratic
polynomial,
parabola |
| The parametric equations of the parabola,
whose axis of symmetry is parallel
to the y-axis
|
|
The quadratic polynomial y
=
a2x2
+ a1x + a0
or y
-
y0
= a2(x
- x0)2,
V(x0,
y0) |
 |
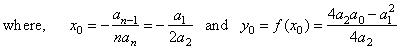| are
the coordinates of translations of the source quadratic y
=
a2x2,
can be transformed to the parametric form
by
substituting x
- x0
= t. |
|
|
|
|
|
| are the
parametric equations of the
quadratic polynomial. |
|
|
|
| Example: Given
are the parametric equations, x
=
t
+ 1
and y
=
-
t2
+ 4,
draw the graph of the curve. |
| Solution:
The equation x
=
t + 1
solve for t
and plug into y
=
- t2 + 4,
thus |
| t
=
x
-
1
=> y
=
- t2 + 4,
y
=
- (x
- 1)2 + 4 |
| i.e., y
-
4
=
- (x
- 1)2
or y
=
- x2 + 2x + 3 translated parabola with the vertex V(x0,
y0),
so V(1,
4). |
 |
|
| The parametric equations of the parabola, whose axis of symmetry is
parallel to the x-axis |
| The
quadratic expression y2
=
2px,
where p
is the distance between focus and directrix, represents
the source or the
vertex form of the conic section called parabola
with the vertex at the origin whose
axis
of symmetry coincide with the x-axis. |
| If
we rewrite the above equation into x
= ay2 then, |
| |
x
= ay2 + by + c
or
x
- x0
= a(y
- y0)2 |
 |
|
|
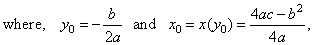| represents
the translation of the parabola in the direction of the coordinate axes
by x0
and y0
i.e.,
V(x0,
y0). |
| Thus,
the parabola, whose axis of symmetry is parallel to the x-axis,
can be transformed to parametric form by
substituting y
- y0
= t
into the above equation. |
|
|
|
|
|
are the parametric equations
of the parabola. |
|
|
|
| Example: Given
is the parabola x
=
- y2 + 2y + 3,
write its parametric equations and draw the graph. |
| Solution:
Rewrite given equation by calculating the coordinates of
translations x0
and y0
or using completing the
square method, we get x
-
4
=
- (y
- 1)2,
where the vertex V(x0,
y0),
so V(4,
1). |
| By
substituting y
- 1
= t
obtained are |
|
|
|
|
|
the parametric equations of the parabola. |
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
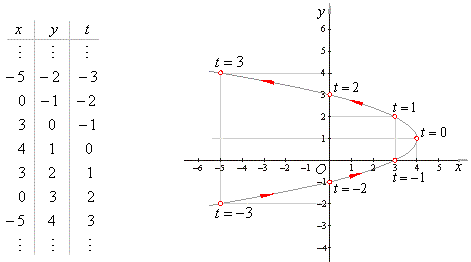| Pre-calculus
contents C |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
