|
|
|
|
Parabola
and Line
|
 Properties of the parabola
Properties of the parabola
|
 Polar of the parabola
Polar of the parabola
|
 Parabola and line, examples
Parabola and line, examples |
|
|
|
|
|
|
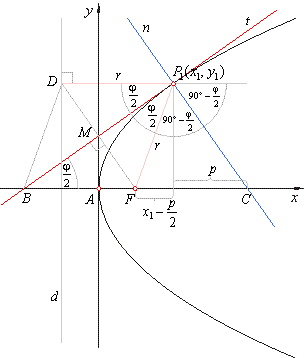
| Properties of the parabola
|
 Using equations of the tangent and normal expressed by coordinates of the tangency points and
the figure above;
Using equations of the tangent and normal expressed by coordinates of the tangency points and
the figure above;
|
|
a) y-intercept
ct
of the tangent equals half of the ordinates of the tangency point, ct
= y1/2. |
b) the projection
AB
of the segment BP1
of the tangent to the x-axis, i.e., to the axis of the parabola, is
equal to twice the abscissa of the tangency
point, so |
|
AB
= St
= 2x1 - the line segment
AB
is called the subtangent. |
|
c) the projection
AC
of the segment CP1
of the normal to the x-axis is equal to the parameter
p, i.e., |
|
AC
= Sn
= p - the line segment
AC
is called the subnormal. |
As points B
and C
are x-intercepts of the tangent and the normal their abscissas we determine by solving
corresponding equations for y =
0, so |
| put y =
0 into equation of the tangent, |
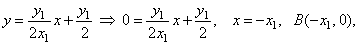 |
|
| put
y =
0 into equation of the normal, |
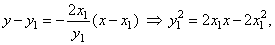 |
|
|
|
| Thus, the focus
F(p/2,
0) bisects the line segment
BC
whose endpoints are x-intercepts of the tangent and
the normal, as shows the figure above. |
|
 The tangent at any point on the parabola bisects the angle
j between focal distance and the perpendicular
to the directrix and is equally inclined to the focal distance and the axis of the parabola.
The tangent at any point on the parabola bisects the angle
j between focal distance and the perpendicular
to the directrix and is equally inclined to the focal distance and the axis of the parabola. |
|
The normal at the tangency
point bisect
the
suplementary angle of the angle
j.
|
|
Since,
DP1
= FP1
= r
= x1
+ p/2,
|
|
and
BF
= FC
= x1
+ p/2
= r, and DP1
|| BC
|
|
then, following triangles are
congruent,
|
|
DBFD
@
DFCP1
@
DFP1D
|
so, the quadrangle
BFP1D
is the rhombus and its
diagonal BP1
bisects the angle j.
|
|
This property is known as the reflective property of the parabola.
|
|
A light rays coming in parallel to the axis of a
parabolic mirror (telescope), are reflected so that they all
pass through the focus. Similarly, rays originating at the
focus (headlight) will be reflected parallel to the axis.
|
|
 |
|
|
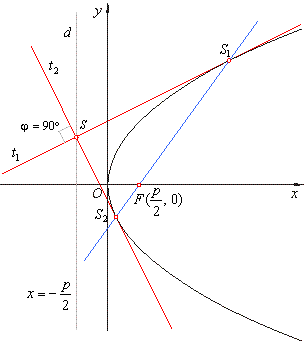
 Tangents drawn at the endpoints of a focal chord intersect at right angles on the
directrix.
Tangents drawn at the endpoints of a focal chord intersect at right angles on the
directrix. |
|
a)
Solving the system of equations of tangents,
|
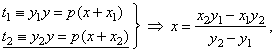
|
|
x
is the abscissa of the intersection S
of tangents.
|
|
The slope of the focal chord line through tangency points,
|
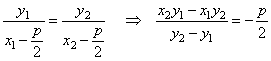
|
|
therefore,
x = -
p/2 is the abscissa
of the intersection S(-
p/2, y) and the equation of the directrix
d.
|
|
b)
The tangent to the parabola which passes through intersection
S, which
lies on the directrix, must satisfy tangency condition,.e.,
|
|
 |
|
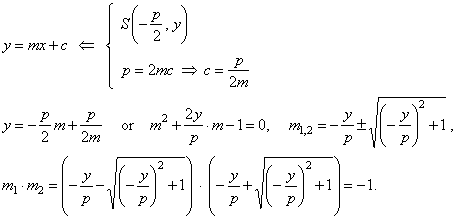 |
| Thus, satisfied is condition for
perpendicularity, m1
· m2
=
-
1 =>
j
=
90°. |
|
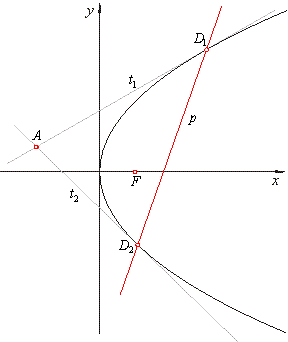
| Polar of the parabola
|
|
The polar p
of a point A(x0, y0), exterior to the parabola
y2 = 2px, is the secant through the contact
points of the
tangents drawn from the point A
to the parabola. |
|
The tangency points
D1(x1, y1)
and D2(x2, y2)
and the point A
satisfy the equations of tangents,
|
|
t1
:: y1y0
= p(x0
+ x1)
and t2
::
y2y0
= p(x0
+ x2).
|
|
Subtracting
t2
-
t1,
|
|
y0(y2
-
y1)
= p[(x0
+ x2)
- (x0
+ x1)]
|
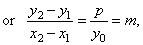
|
|
obtained is the slope of the polar. By plugging the slope into equation of the line through the given point
|
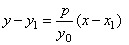 |
or
y0y
= y1y0
+ px -
px1 |
|
|
since y1y0
= p(x0
+ x1),
|
| then
|
y0y
= p(x
+ x0) |
the
equation of the
polar.
|
|
|
 |
|
|
| Parabola and line, examples |
| Example:
Find the angle between tangents drawn at intersection points of a line and the parabola
y2 = 2px
if the line passes through the focus F(7/4,
0) and its slope
m =
4/3. |
|
Solution:
As F(p/2,
0)
then, p/2 =
7/4 and the equation
of the parabola y2 =
7x.
|
| By plugging
m =
4/3 and
F(7/4,
0) into
the equation of the line
y
-
y1 =
m(x
-
x1)
obtained is
|
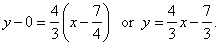
|
|
Intersections of the line and the parabola,
|
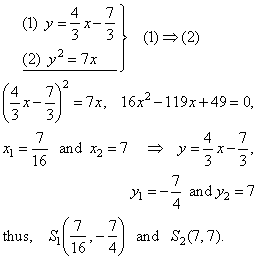
|
|
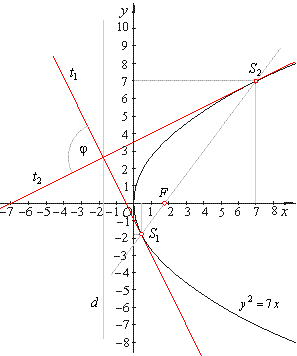 |
|
|
Substituting
coordinates of S1
and S2
in
|
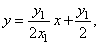 |
we
get the equation of tangents, |
|
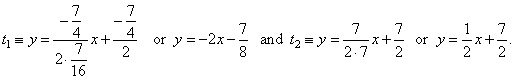 |
| Slopes of tangents satisfy the perpendicularity
condition, |
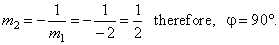 |
|
|
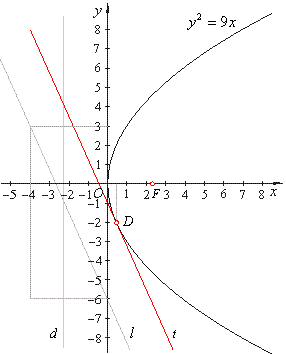
| Example:
Find the point on the parabola
y2 = 9x closest to the line
9x + 4y + 24 =
0. |
|
Solution:
The tangency point of the tangent parallel to
the given line is the closest point.
|
|
9x + 4y +
24 = 0
=> y =
-(9/4)x
-
6, mt =
-
9/4
|
|
The slope of the tangent must satisfy tangency
condition
of the parabola,
|
|
p = 2mc
<= mt =
-
9/4, p
=
9/2
|
|
9/2 = 2 · (-9/4)
· c
=>
c
= -
1
|
|
therefore, the
tangent t
:: y =
-(9/4)x
-
1.
|
|
The solution
to the system of equations of the tangent and the parabola
gives the tangency point, that
is
|
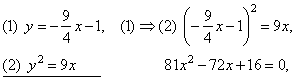
|
|
 |
|
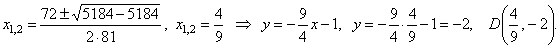 |
|
| Example:
Given is the polar
4x + y + 12 =
0 of the parabola
y2 = -4x, find coordinates of the pole and
write equations of the corresponding tangents. |
|
Solution:
Intersections of the polar and the parabola are the
tangency points of tangents drawn from the pole P.
Thus, by solving the system of equations of the polar and the parabola
we get the tangency points. |
|
(1) 4x + y +
12 =
0, (1) =>
(2) (-4x
-
12)2 = -4x
|
|
(2) y2 =
-4x
4x2
+ 25x + 36 =
0,
|
|
|
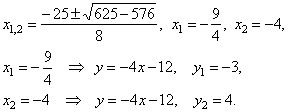
|
|
Equation of the tangent at the point on the parabola,
|
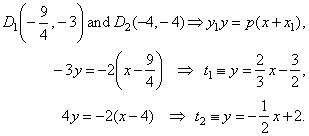
|
|
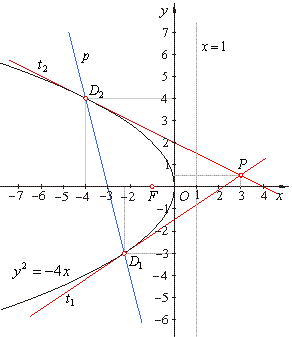 |
|
|
The intersection of tangents is the pole P.
Therefore, we solve the system formed by their equations, |
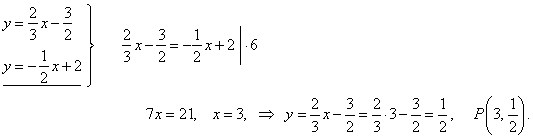 |
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
H |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |