|
|
|
|
Parabola
|
 Parametric equations of the parabola
Parametric equations of the parabola
|
 Parabola examples
Parabola examples
|
|
|
|
|
|
|
| Parametric equations of the parabola
|
|
Parametric equations of the parabola
y2 =
4ax
with the vertex A
at the origin and the focus F(a,
0), and of its translation (y
-
y0)2 =
4a(x
-
x0)
with the vertex A(x0, y0)
and the focus F(x0
+ a, y0)
written |
| respectively
are, |
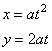 |
|
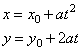 |
|
|
|
Parametric equations of the parabola
x2 =
4ay
with the vertex A
at the origin and the focus F(0,
a), and of its translation
(x
-
x0)2 =
4a(y
-
y0)
with the vertex A(x0, y0)
and the focus F(y0,
y0
+ a) written |
| respectively
are, |
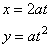 |
|
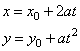 |
|
|
|
|
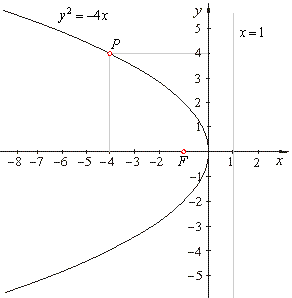
| Example:
Write equation of the parabola
y2 = 2px
passing through the point P(-4,
4) and find the focus,
the equation of the directrix and draw its graph. |
|
|
|
Solution:
The coordinates of the point P
must satisfy the equation of the parabola
|
|
P(-4,
4)
=>
y2 =
2px
|
|
42 = 2p(-4)
=> p =
-2
|
|
thus, the
equation of the parabola y2 =
-4x.
|
|
The coordinate
of the focus,
|
|
since F(p/2,
0) then
F(-1,
0).
|
|
The equation of the directrix,
as x =
- p/2,
x =
1.
|
|
 |
|
|
| Example:
Into a parabola y2 =
2px
inscribed is an equilateral triangle whose one vertex coincides with the
vertex of the parabola and whose area A =
243Ö3.
Determine equation of the parabola and remaining vertices of the triangle. |
Solution:
Let write coordinates of a point
P
of the
parabola as elements of the equilateral triangle
|

|
|
As the point P
lies on the parabola then
|
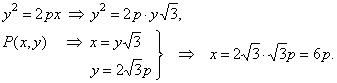
|
The area of the equilateral triangle we express by
coordinates of
P
|
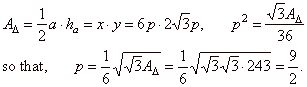
|
|
 |
|
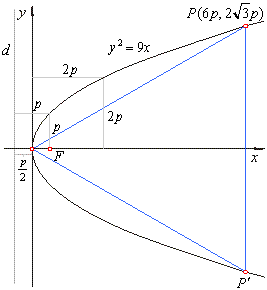
| Show the parameter of the parabola by the side of the triangle, |
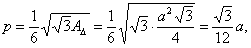 |
|
| and
the vertices of the triangle P(6p,
2Ö3p) and
P'(6p,
-2Ö3p)
so that, P(27,
9Ö3) and
P'(27,
-9Ö3). |
| Therefore,
the equation of the parabola y2 =
2px or
y2 = 9x. |
|
| Example:
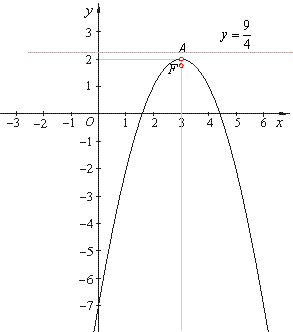
Find the vertex, the focus and the equation of the directrix and draw the graph of the parabola |
| y =
-x2
+ 6x -
7. |
|
Solution:
Rewrite
the equation of the parabola in the translatable form
|
|
(x
-
x0)2 = 2p(y
-
y0) or
y
-
y0 = a(x
-
x0)2
|
|
so, y =
-x2
+ 6x -
7
=> y =
-(x2
-
6x) -
7
|
|
y =
-[(x
-
3)2
-
9] -
7
|
|
y
-
y0 = a(x
-
x0)2,
y
-
2 = -(x
-
3)2,
a
= -1.
|
|
The vertex of the parabola
A(x0, y0),
or
A(3, 2).
|
|
The focus
F(x0,
y0 + 1/(4a)),
or
F(3,
7/4).
|
|
The equation of the directrix,
|
|
y =
y0 -
1/(4a),
y = 2 +
1/4 or
y =
9/4.
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
H |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|