|
|
Systems of Linear
Equations |
| Solving systems of
equations using matrices |
| A
system of linear equations is a set of n
equations in n
unknowns (variables) of the form |
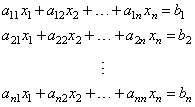 |
| where,
the unknowns are denoted by x1,
x2, ... xn,
the coefficients (aij)
and constants (bi)
are given values. |
| The
system of equations above can be written in matrix form as |
| |
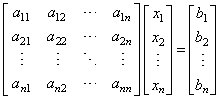 |
or |
Ax =
b |
|
|
| where,
A
is matrix of the coefficients (aij), x
is a vector of n
unknowns and b
is a vector of n
constants. |
|
| Inverse
matrix method |
| The
matrix equation Ax =
b,
where A
is an n
´
n
regular matrix (det(A)
is not 0), multiplied by A-1
gives |
| A-1Ax =
A-1b |
| since,
A-1A =
I by definition and Ix =
x, where I
is the identity matrix, as |
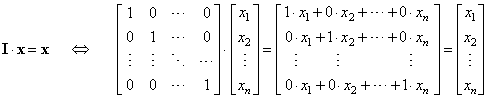 |
| then |
| x =
A-1b. |
| Thus,
the inverse matrix method uses this matrix equation to find the
solution to the system of equations directly. |
|
| Example:
Find the solution of the given three simultaneous equations
using the inverse matrix method.
|
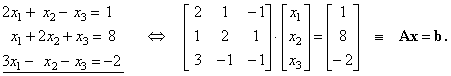 |
| The given
equations are written as the equivalent matrix equation. |
| Then,
both sides of the above matrix equation we multiply by the
inverse of the coefficient matrix A
(calculation
of which is shown in the previous example), |
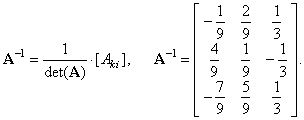 |
| Since.
A-1A =
I and Ix =
x, then |
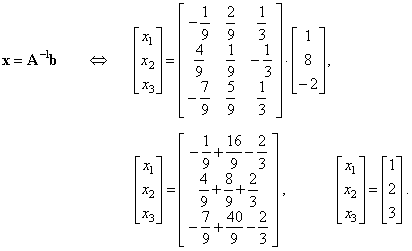 |
| Therefore,
the solution is, x1
= 1, x2 = 2
and x3
= 3. |
|
| Cramer’s Rule and
inverse
matrix method correlation |
| Cramer's
Rule says that a system of n
linear equations in n
unknowns, |
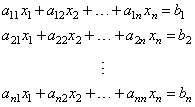 |
| will
have a unique solution if the determinant of the coefficient
matrix det(A)
= A = | aik | is
nonzero, and in this
case, the value of the unknown xk
is given by the
expression |
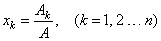 |
| where
the numerator Ak
is equal to the determinant A
of the matrix A
that results when the kth
column (the coefficients
of the unknown to be found) of the coefficient matrix is
replaced by the column of constants, b1,
b2,
. . . , bn. |
|
| Let
show that Cramer's Rule, to find the value of the unknown xk,
coincide with the solution given by the matrix
equation x =
A-1b. |
|
| That
is, by expanding the determinant Ak
by the kth
column we get |
| Ak = b1A1k
+ b2A2k
+ . . . + bnAnk |
| where, A1k, A2k,
. . . , Ank
are the cofactors of the entries, b1,
b2,
. . . , bn,
that are the same as the cofactors
of the entries, a1k,
a2k,
. . . , ank,
of the determinant A =
det(A) or the matrix A. |
| To
find the value of unknown xk
from x =
A-1b
we should calculate the scalar product of the kth
row vector of A-1
and the column vector b. |
| Therefore,
if aik
denotes the entries of A-1
then |
| xk =
ak1b1
+ ak2b2
+ . . . + aknbn. |
| Recall
that |
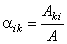 |
where Aki
denotes the kith
entry of
the transpose of the cofactor matrix. |
|
|
| As
the transposition interchange rows and columns, the above expression for the unknown xk
can also be written as |
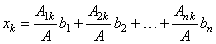 |
| what
coincide with |
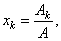 |
where Ak = b1A1k
+ b2A2k
+ . . . + bnAnk. |
|
|
| That
proves the correlation between solution given by Cramer's Rule
and the solution given by the matrix
equation x =
A-1b. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
K |
|
 |
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|