|
|
|
|
The Binomial Theorem
|
 Factorial
Factorial
|
 Binomial coefficients and
Pascal's triangle
Binomial coefficients and
Pascal's triangle |
 The binomial theorem, sigma notation
and binomial expansion
algorithm
The binomial theorem, sigma notation
and binomial expansion
algorithm |
|
The
binomial theorem and binomial expansion algorithm examples |
|
|
|
|
|
|
|
|
The Binomial Theorem
|
|
Factorial
|
| The
factorial is defined for a positive integer n,
denoted n!
represents the product of all positive integers less than or equal to
n, |
|
n! = n · (n -
1) · · · 2 · 1. |
|
The first few factorials are, 1!
= 1, 2!
= 2 · 1
= 2, 3!
= 3 · 2 · 1 =
6, 4!
= 4 · 3
· 2 · 1
= 24, and so on.
|
|
By the definition, 0!
= 1. |
| So
for
example, n!
shows the number of ordered arrangements or permutations of n
objects, that is, on how many ways n
distinct objects can be arranged in a row. |
| Thus,
for example four digits 1, 2, 3, 4 can be arranged in 4!
= 24 ways, as is shown below |
|
1, 2, 3, 4
2, 1, 3, 4
3, 1, 2, 4
4, 1, 2, 3 |
|
1, 2, 4, 3
2, 1, 4, 3
3, 1, 4, 2
4, 1, 3, 2 |
|
1, 3, 2, 4
2, 3, 1, 4
3, 2, 1, 4
4, 2, 1, 3 |
|
1, 3, 4, 2
2, 3, 4, 1
3, 2, 4, 1
4, 2, 3, 1 |
|
1, 4, 2, 3
2, 4, 1, 3
3, 4, 1, 2
4, 3, 1, 2 |
|
1, 4, 3, 2
2, 4, 3, 1
3, 4, 2, 1
4, 3, 2, 1 |
|
| Binomial coefficients
and
Pascal's triangle |
| A
binomial coefficient is a numerical factor that multiply the successive
terms in the expansion of the binomial (a
+ b)n,
for integral n,
written |
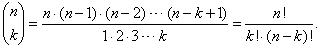 |
| So
that, the general term, or the (k
+ 1)th
term, in the expansion of (a
+ b)n, |
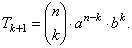 |
| For
example, |
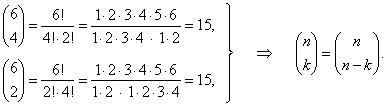 |
|
| The
binomial coefficients can also be
obtained by using Pascal's triangle. |
| The
triangular array of integers, with 1 at the
apex, in which each number is the sum of the two
numbers above it in the preceding row, as is
shown in the initial segment in the diagram, is
called Pascal's triangle. |
| The
binomial coefficients refer
to the nth
row, kth
element in Pascal's triangle as shows the right
diagram. |
| So,
for example the 6th
row of the triangle
contains the sequence of the coefficients of a
binomial of the 6th power. |
|
| n |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
| 2 |
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
|
|
| 3 |
|
|
|
|
1 |
|
3 |
|
3 |
|
1 |
|
|
|
|
| 4 |
|
|
|
1 |
|
4 |
|
6 |
|
4 |
|
1 |
|
|
|
| 5 |
|
|
1 |
|
5 |
|
10 |
|
10 |
|
5 |
|
1 |
|
|
| 6 |
|
1 |
|
6 |
|
15 |
|
20 |
|
15 |
|
6 |
|
1 |
|
| - |
|
0th |
- |
1st |
- |
2nd |
- |
3rd |
- |
4th |
- |
5th |
- |
6th |
1 |
|
|
|
| A
binomial coefficient equals the number of ways that r
objects can be selected from n
objects without regard to order, called combinations and noted C(n,
r) or Cnr. |
| For
example, the number of distinct combinations of three digits selected from
1, 2, 3, 4, 5 is |
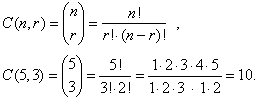 |
| 1
2 3 2
3 4 3
4 5 |
| 1
2 4 2
3 5 |
| 1
2 5 2
4 5 |
| 1
3 4 |
| 1
3 5 |
| 1
4 5 |
|
|
|
|
The binomial theorem, sigma notation
and binomial expansion
algorithm |
| The
theorem that shows the form of the expansion of any positive integral
power of a binomial (a
+ b)n
to a polynomial with n
+ 1 terms, |
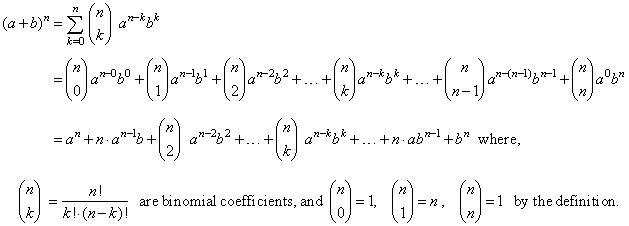 |
|
|
|
The
binomial theorem and binomial expansion algorithm examples
|
|
|
|
| Example: Find
the 4th term of the binomial
expansion (a - x)5. |
|
|
| Or,
we can use the formula to find (k
+ 1)th
term. |
|
|
| Since, n =
5
and k
+ 1 = 4 =>
k
=
3 then by plugging these values into |
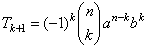 |
|
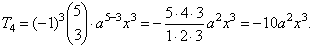 |
|
| Example: Find
the middle
term of the binomial
expansion |
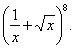 |
|
|
|
|
| Example: Find
the 7th term of the binomial
expansion |
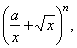 |
if the coefficient of the third
term |
|
| relates
to the coefficient of the second term as 9 : 2. |
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
K |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|