|
| Conic
Sections |
|
|
|
|
Hyperbola
|
 Definition and construction
of the hyperbola
Definition and construction
of the hyperbola
|
|
Construction of the hyperbola
|
 Equation of the hyperbola
Equation of the hyperbola
|
|
Properties of the hyperbola
|
|
Examining equation of the hyperbola
|
|
Examples of hyperbola |
|
|
|
|
|
|
| Definition and construction
of the hyperbola
|
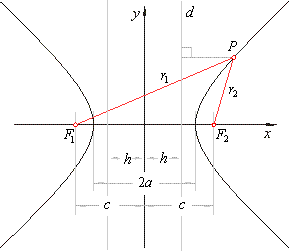
| The set of points in the plane whose distance from two fixed points (foci,
F1
and
F2
) has a constant difference 2a
is called the hyperbola. |
| Therefore, for every point of the
hyperbola |
| | F1P
-
F2P
|
= 2a |
| with the focal distance
|F1F2|
= 2c, so that
a
< c. |
| The ratio
e =
c/a,
e
> 1 |
|
is called eccentricity of the hyperbola.
|
|
The hyperbola can also be defined as the locus of points the ratio of whose distances from the focus, to a vertical line known as the directrix, is a constant e, where
|
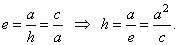
|
|
 |
|
|
| Construction of the hyperbola
|
Given are values,
a
and c. Draw two equal arcs of an
arbitrary radius r1
=
A1'
R,
|
| so that
r1
>
a + c
or r1
>
2a +
(c
-
a),
|
| one centered at
F1
and another at
F2. |
| Then, these arcs intersect by two arcs of the radius
|
|
r2 =
A2'
R =
r1
-
2a,
drawn from both foci.
|
| Thus, obtained are four points of the hyperbola.
|
|
Repeating this procedure by changing radii of arcs, we can get enough points of the hyperbola.
|
|
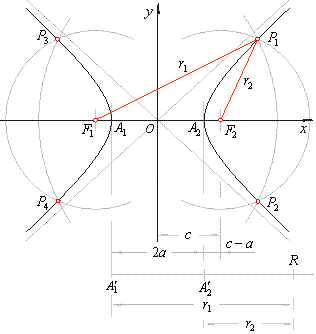
It is obvious from the construction that the hyperbola
has two axes of symmetry which intersects at the center of the hyperbola. The axis which coincides with the
x-axis
is the transverse or the
real axis, the other which lies on the
y-axis is the
conjugate or the
imaginary
axis.
|
|
 |
|
|
| Equation of the hyperbola
|
| If in the direction of the axes we introduce a coordinate system so that the center of the hyperbola
coincides with the origin, then coordinates of foci are |
| F1(-c,
0)
and
F2(c,
0). |
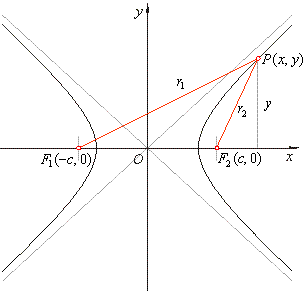
| For every point
P(x, y)
of the hyperbola, according to |
|
definition | r1
-
r2
|
= 2a, |
| using the formula for the distance of two points,
|
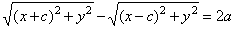 |
|
after squaring
and reducing
|
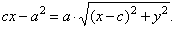
|
|
By squaring again and grouping
|
|
(c2 -
a2) · x2 -
a2y2
= a2
·
(c2 -
a2).
|
|
 |
|
| Substituting
c2 -
a2
= b2
or |
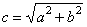 |
obtained is |
b2x2
-
a2y2
= a2b2 |
equation of the hyperbola, |
|
| and after division by
a2b2 ,
|
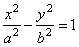 |
the standard equation of the hyperbola. |
|
|
| Examining equation of the hyperbola
|
| The hyperbola is determined by parameters,
a
and
b, where
a
is the semi-major axis (or transverse
semi-axis) and b
is the
semi-minor axis (or conjugate
semi-axis). The intersection points of the hyperbola with coordinate axes we determine from its equation, |
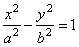 |
| by
setting, y
= 0
=>
x
= ± a |
| the
hyperbola has intercepts with the
x-axis
at vertices
|
| A1(-a,
0)
and
A2(a,
0). |
| The
segment A1A2
= 2a
is called the
transverse axis.
|
| By
setting, x
= 0
=> y
= ± b·i
there are no
intercepts with y-axis.
|
|
Perpendicular to the transverse axis at the midpoint is the
conjugate axis, whose length is
B1B2
= 2b.
|
|
The hyperbola
consists of two branches.
|
|
If we solve the equation of the hyperbola for
y,
|
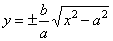
|
|
 |
|
| it follows that the value of the square root will be real if
| x |
>
a. That is, if the absolute value of
x
is less then a,
then y
is an imaginary number, so that in the interval of x
Î
(-a,
a) there are no points of the hyperbola. |
As the hyperbola is symmetric to both coordinate axes, we can examine behavior of only part of the curve
located at the first quadrant for values of x
>
a. |
| Rewrite the above equation so that it represents only the
positive values of the curve in this interval of x, so |
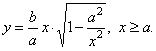 |
| Since the value of
x increases and tends to infinity,
x
®
oo
, then the term |
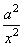 |
tends to zero, so that |
|
| value of the square root tends to
1
and the equation of the hyperbola changes to |
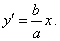 |
|
|
| This equation shows that points
of the hyperbola become closer and closer to this line for large values of
x. |
From the above equation of the hyperbola we see that for every value
x
> a, the value of the square root is
less then 1, it means that the ordinate
y
of every point of the hyperbole is less then the ordinate
y’ of the
corresponding point of the line. |
| We also see that as
x
increases, the difference of ordinates, y
and y’ becomes smaller, what means that points
of the hyperbola become closer to this line. |
| |
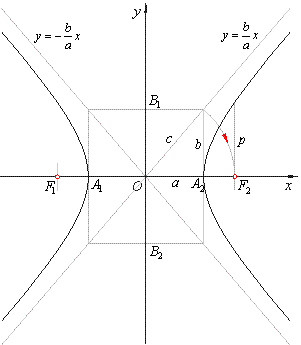
The
lines, |
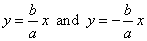 |
are the asymptotes of the hyperbola. |
|
The asymptotes of a hyperbola coincide with the diagonals of the rectangle whose center is the center of the
curve, and whose sides are parallel and equal to the length 2a and
2b, of the axes of the curve, as
shows the above figure. |
| From
the equation of the hyperbola |
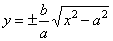 |
for
x
= ± c,
obtained is |
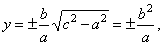 |
|
| the
semi-latus rectum p. |
| The length of
p can also be calculated from the right triangle with legs
p and
2c,
whose hypotenuse is p + 2a, according to the definition of the hyperbola. |
| |
The latus rectum |
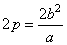 |
|
|
| are the chords perpendicular to the transverse axis and passing through the foci. |
| The hyperbola which has for its transverse and conjugate axes the transverse and conjugate axes of another |
| hyperbola, is said to be the
conjugate
hyperbola. So the hyperbolas, |
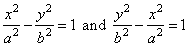 |
are |
|
| conjugate
hyperbolas of each other. |
| A given hyperbola and its conjugate are constructed on the same reference rectangle.
Thus, they have the common asymptotes and their foci lie on a circle. |
|
| Examples
of hyperbola |
Example:
Given is the hyperbola
4x2 -
9y2 = 36,
determine the semi-axes, equations of the asymptotes,
coordinates of foci, the eccentricity and the semi-latus rectum.
|
Solution:
Put the equation in the standard form to
determine the semi-axes, thus
|
|
4x2
-
9y2 = 36 | ¸
36
|
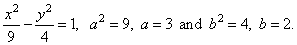
|
| Asymptotes, |
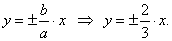 |
|
| Applying, |
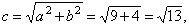 |
|
|
coordinates of foci, F1(-Ö13,
0) and
F2(Ö13,
0).
|
|
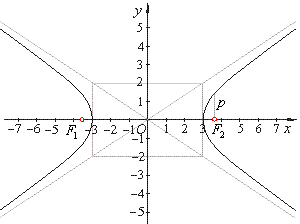 |
|
| The eccentricity, |
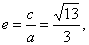 |
and the
semi-latus rectum,
|
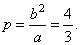 |
|
|
| Example:
Write equation of a hyperbola with the focus at
F2(5,
0) and whose asymptotes are, |
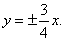 |
|
|
|
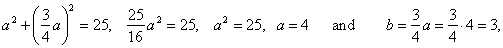 |
| Therefore,
the equation of the hyperbola,
|
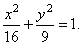 |
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
H |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |