|
The graph of
the
cosecant function |
|
The graph of
the
secant function |
|
The
graph of the
arc-cosecant and the
arc-secant function |
|
|
|
|
|
|
| Algebraic
and transcendental functions |
| Elementary
functions are, Algebraic functions
and Transcendental functions |
|
| Trigonometric
(cyclometric) functions and inverse trigonometric functions (arc
functions) |
| Trigonometric functions are defined as the ratios of the sides of a right
triangle containing the angle equal to the argument of the
function in radians.
|
| Or
more generally for real arguments, trigonometric
functions are defined in terms of the coordinates of the
terminal point Q of
the arc
(or angle) of the unit circle with the initial point at P(1,
0). |
|
|
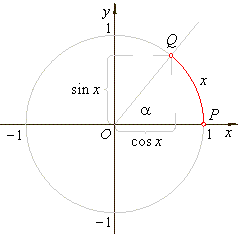 |
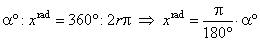 |
| sin2x
+ cos2x
= 1 |
|
|
|
| The
graphs of the trigonometric
functions and inverse trigonometric functions or arc-functions |
|
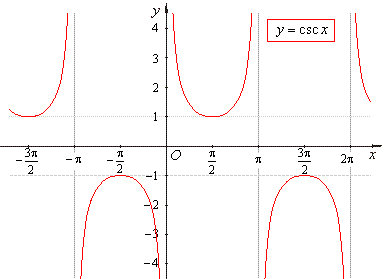
- The
cosecant function
y
= csc x
is the reciprocal of the sine function. |
| In
a right-angled triangle the
cosecant function is equal to the ratio of the length of the
hypotenuse to that of the side opposite to the given angle. |
|
| The
graph of the
cosecant function |
 |
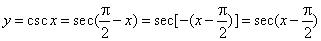 |
|
|
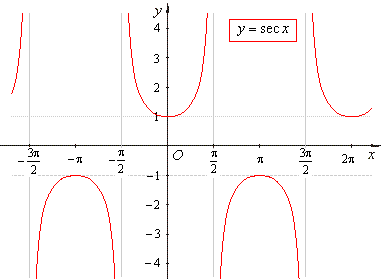
- The
secant function
y
= sec x
is the reciprocal of the cosine function. |
| In
a right-angled triangle the secant function is equal to the
ratio of the length of the hypotenuse to that of the side
adjacent to the given angle. |
|
| The
graph of the
secant function |
 |
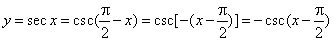 |
|
|
- The
arc-cosecant function
y
= csc-1x
or y
= arccsc x
is the inverse of the cosecant function, so that its value for any
argument is an arc (angle) whose cosecant equals the given
argument. |
| That
is, y
= csc-1x
if and only if x
= csc
y.
For
example, |
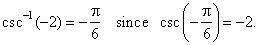 |
|
|
Thus, the arc-cosecant
function is defined for arguments less than -1
or greater than 1, and its principal
values are by
convention taken to be those between -p/2
and p/2. |
|
|
- The
arc-secant function
y
= sec-1x
or y
= arcsec x
is the inverse of the secant function, so that its value for any
argument is an arc (angle) whose secant equals the given
argument. |
| That
is, y
= sec-1x
if and only if x
= sec
y.
For
example, |
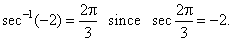 |
|
|
Thus, the arc-secant
function is defined for arguments less than -1
or greater than 1, and its principal
values are by
convention taken to be those between 0
and p. |
|
| The
graph of the
arc-cosecant and the
arc-secant function |
|
|
|
|
|
|
|
|