|
|
 Quadratic
function y
=
a2x2
+
a1x + a0
Quadratic
function y
=
a2x2
+
a1x + a0 |
|
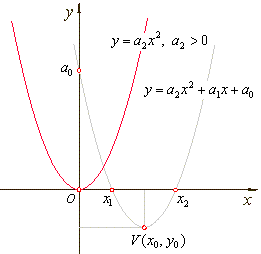
Graphing source and translated quadratic
function |
|
|
|
|
|
|
| Quadratic
function y
=
a2x2
+
a1x + a0 |
| 1)
Let calculate the
coordinates of translations of quadratic function using the
formulas, |
| substitute
n
= 2 in |
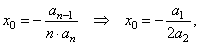 |
|
|
| then |
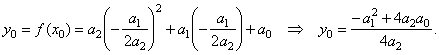 |
|
|
| 2)
To
get the source quadratic function we should plug the coordinates
of translations (with changed signs)
into the general form
of the quadratic,
i.e., |
 |
| after
expanding and reducing obtained is |
|
y
=
a2x2
the source quadratic function. |
| 3)
Inversely, by plugging the coordinates of translations into the source quadratic function |
|
y
-
y0
= a2(x
-
x0)2, |
|
|
| and
after
expanding and reducing we obtain |
|
y
=
a2x2
+ a1x
+ a0
the quadratic function
in the general form. |
| Graphing
source and translated quadratic
function |
| f
(x)
=
y
=
a2x2
+
a1x + a0
or y
-
y0
= a2(x
+ x0)2, |
| where |
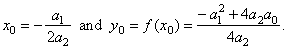 |
|
| By
setting x0
= 0 and y0
= 0
obtained is |
| the
source quadratic
y
= a2x2
. |
|
| If
a2
·
y0
< 0
then
the roots are |
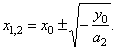 |
|
|
The turning point V(x0
, y0
).
|
|
 |
|
|
| According
to mathematical induction we can examine any
n-degree
polynomial function using shown method. |
| Therefore,
the polynomial f
(x) =
y = anxn
+ an-1xn-1
+ an-2xn-2
+
.
. .
+
a2x2
+
a1x + a0 |
| we can
write as
|
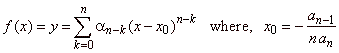 |
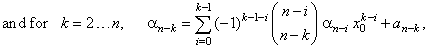 |
|
while, for k = 0, an
=
an, |
|
|
|
and from which, for k =
n,
a0
=
f
(x0)
= y0. |
|
| Thus,
expanded form of the above
sum is |
| y
- y0
= an(x
- x0)n
+ an-2(x
- x0)n-2
+
.
. . +
a2(x
- x0)2
+ a1(x
- x0) |
| where
x0
and y0
are coordinates of translations
of the graph of the source polynomial |
| fs(x)
= anxn
+ an-2xn-2
+
.
. . +
a2x2
+ a1x
|
| in
the direction of the x-axis
and the y-axis
of a Cartesian coordinate system. |
| Therefore,
every given polynomial written in the general form can be
transformed into translatable form by calculating the
coordinates of translations x0
and y0
and the coefficients a
of its source function. |
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
D |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |