|
|
|
Exponential and Logarithmic
Functions and Equations
|
 Exponential and logarithmic equations
Exponential and logarithmic equations
|
|
Solving exponential
and logarithmic equations |
|
Exponential equations
|
|
Logarithmic equations
|
|
|
|
|
|
|
| Exponential and logarithmic equations
|
| Exponential equations
|
| In
exponential equations the variable that has to be solved for is in
the exponent. |
| To
solve an exponential equation, rewrite the given equation to get
all powers (exponentials) with the same base, or use
logarithms when solving the exponential equation. |
|
| Example: Solve
3x
- 1
= 81. |
| Solution:
3x
- 1
= 81 |
|
3x
- 1
= 34 |
|
x
- 1
= 4 =>
x
= 5. |
|
| Example: Solve
0.25x
= 43x
- 2. |
|
|
|
| Example: Solve
43x
+ 2
= 64 · 22x
- 4. |
| Solution:
42 · 43x
= 43 · 22(x
- 2)
| ¸
42 |
|
43x
= 41 + x
- 2 |
|
3x = x
- 1 |
|
2x
= - 1
=>
x
= - 1/2. |
|
| Example: Solve
4x
+ 2
+ 4x
+ 1
+ 4x
-1
= 3x
+ 3
+ 3x
+ 2. |
|
|
|
| Example:
Solve 4x
-
2 =
5x. |
|
|
|
| Example: Solve |
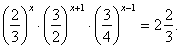 |
|
|
|
|
| Example: Solve 3
· 4x
+ 2 · 9x
= 5 ·
6x.
|
|
|
|
| Logarithmic equations
|
| As
logarithmic equations contain a logarithm of variable quantity,
we use rules and properties of logarithms to solve a logarithm
equation. |
|
| Example: Solve log
x = -2. |
| Solution:
log
x = log10-2
=>
x = 10-2
= 0.01. |
|
| Example: Solve log2
(log3 x) = 1. |
| Solution:
log3 x
= 21
=>
x = 32
= 9. |
|
| Example: Solve log
(x + 5) -
log
(2x -
3) = 2 · log 2. |
|
|
|
| Example: Solve log
(log
x) + log
(log
x3 -
2) = 0. |
|
|
|
| Example: Solve
x
log x -
2 =
1000. |
|
|
|
|
|
|
|