Exponential and Logarithmic Functions and Equations
      Translated logarithmic and exponential functions
         Rules and properties of logarithms
         Natural logarithm and common logarithm conversions
         Changing the base – different logarithmic identities
Rules and properties of logarithms
A logarithm is the exponent (the power) to which a base must be raised to yield a given number, that is
y = loga x  if   x = a y.
Examples:  
 
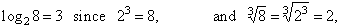Notation: Common logarithms of x, log10 x (to the base 10) are often written log x, without the base explicitly indicated while, Natural logarithms, loge x (to the base e, where e = 2,718218... ), are written ln x.
Therefore,
loga ax = x 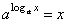loga a = 1 loga 1 = 0
Logarithms are used to simplify multiplication, division and exponentiation so that,
   loga (m · n) = loga m + loga n    
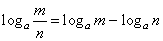  loga mn = n · loga m    
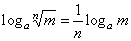Example:  Using the rules of logarithms find the value of x.
 Solution:    
 
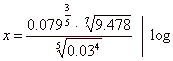Changing the base – different logarithmic identities
Using the identity
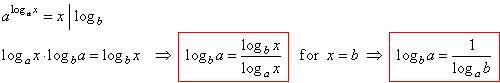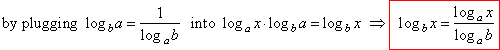In a similar way
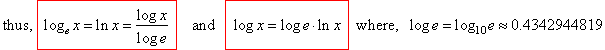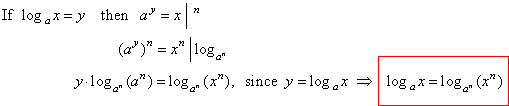therefore,    
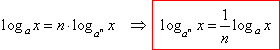Similarly,
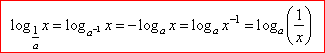and
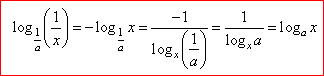Example:   If   log 2 x = 7  then  log 4 2x = ?.
Solution:
Example:   If   a = log 10 2  then  log 10 25 = ?.
Solution:
Example:   Find the value of the expression
Solution:
Example:   Find the value of the expression
Solution:
Example:   Find the value of the expression
Solution:
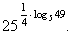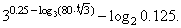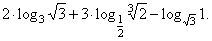Example:    If   a = log 5 and  b = log 3  then  log 30 8 = ?.
Solution:
Example:   Find the value of the expression
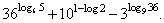Solution:
Pre-calculus contents F
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.