|
|
|
|
Simultaneous
Linear Equations
|
 System
of linear equations word problems
System
of linear equations word problems
|
 Solving
systems of equations graphically
Solving
systems of equations graphically
|
|
Independent
equations, inconsistent equations and dependent equations
|
|
|
|
|
|
|
|
|
System
of linear equations word problems
|
|
Example: A two-digit number enlarges by nine when its digits reverse. The
same two-digit number divided by
sum of its digits gives quotient 5
and reminder 4. Find the two-digit number.
|
|
Solution:
Let
x be ten's digit and
y
units' digit, then 10x+
y is a two-digit
number.
|
|
Then, written are conditions of the given problem:
|
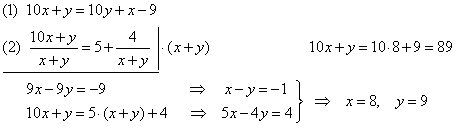
|
|
|
|
Example: An isosceles triangle with the sides 6 cm longer then base has the
perimeter 48 cm.
|
|
What is the length of its base and the sides?
|
|
Solution:
|
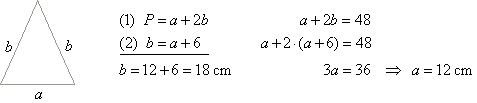 |
|
|
|
|
Example: The perimeter of a rectangle is 42 cm. The ratio between its width
and the length is 3 : 4.
|
|
Find the length and width of the rectangle.
|
|
Solution:
|
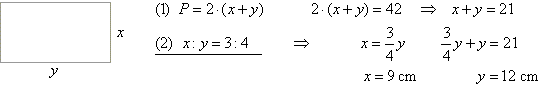 |
|
|
|
|
Solving
systems of equations graphically
|
|
The system of two equations in two unknowns can be represented
graphically in the Cartesian plane as two
|
|
lines l1
and l2.
|
| |
| |
| |
| l1
::
a1x+ b1y
+ c1 = 0 |
| l2
::
a2x
+ b2y
+ c2 = 0 |
| |
| |
| |
|
|
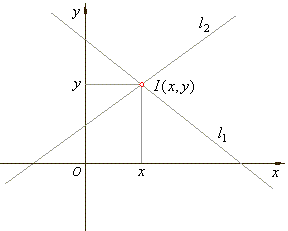 |
|
|
|
The coordinates (x,
y)
of the intersection of the two lines are the
values of the variables that make both equations true.
|
|
|
|
Independent
equations, inconsistent equations and dependent equations
|
|
There are three possibilities:
|
| a) Independent equations, the lines intersect
in one point. There is a unique solution if |
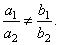 |
|
|
| b)
Inconsistent equations, the lines are parallel but distinct (have the same slope), that is |
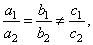 |
|
and there is
no solution. |
|
|
| c)
Dependent equations, equations describe the same line, that is |
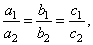 |
thus, there are an
|
|
infinite number of solutions to the system.
|
|
|
|
|
|
| Example:
Solve graphically given system of
linear equations:
|
|
Solution:
|
| l1
::
2x
+ 3y -
4 = 0 |
| l2
::
-x
+ 2y -
5 = 0 |
| Coefficients
satisfy the condition: |
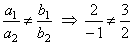 |
| so, the
lines intersect. |
|
|
|
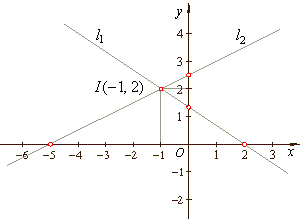 |
|
|
|
Solve equation y
= 0 to get the
x-intercept, and
x
= 0 to get the
y-intercept.
|
|
Thus, obtained are the points, (2,
0) and
(0,
4/3) of
the line l1, and
(-5,
0) and
(0,
5/2) of
the line l2.
|
|
The
lines intersect at (-1,
2).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
|
|
Copyright © 2004 - 2020, Nabla Ltd.
All rights reserved.
|