|
| Cubic
functions |
| Using the same method we can analyze the third degree polynomial or cubic functions. |
| y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0), |
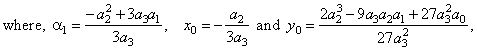 |
| By
setting x0
=
0 and y0
= 0 we get
the source cubic function
y
= a3x3
+
a1x
where a1=
tanat |
| Coordinates
of the point of inflection coincide with the coordinates of
translations, i.e., I
(x0,
y0).
|
| The source cubic functions are
odd functions. |
| Graphs of odd functions are
symmetric about the origin that is, such functions change
the sign but not absolute value when the sign of the independent variable is
changed, so that f
(x)
=
-
f (-x). |
| That
is, change of the sign of the independent variable of a function
reflects the graph of the function about the y-axis,
while change of the sign of a function reflects the graph of the
function about the x-axis. |
| The
graphs of
the translated cubic functions are symmetric about its
point of inflection. |
|
| As
shows the figure below there are three types of cubic
functions: |
| type
1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3
where
a1
= 0 |
|
|
| therefore,
its source function y
=
a3x3,
and the tangent line
through the point of
inflection is horizontal. |
| type
2/1 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0),
where a3a1>
0 |
|
| whose
slope of the tangent line through the point of inflection is
positive and equal a1. |
| type
2/2 |
y
=
a3x3
+ a2x2
+ a1x
+ a0 or
y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0),
where a3a1<
0 |
|
| whose
slope of the tangent line through the point of inflection is
negative and is equal a1. |
| The
graph of its source function has three zeros and two turning
points at |
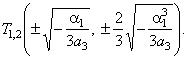 |
|
| |
| Graphs
of cubic functions |
|
|
|
|
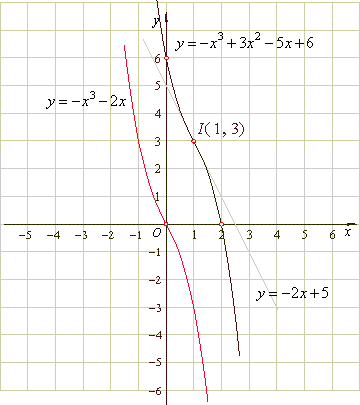
| Example:
Find the coordinates of
translations, the zero point, the point of inflection and draw
graphs of
the cubic function y
=
-
x3
+ 3x2
-
5x
+
6
and its source function. |
| Solution:
1)
Calculate the coordinates of translations
|
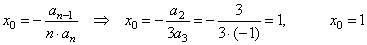 |
|
y0
= f(x0)
=>
y0
= f(1)
=
-13
+ 3 · 12
-
5
· 1
+
6 =
3,
y0
= 3 |
| Therefore,
the point of inflection I
(1,
3). |
| 2)
To
get the source cubic function, plug the coordinates
of translations into the general
form
of the cubic, |
| y
+ y0
=
a3(x
+
x0)3
+ a2(x
+
x0)2
+ a1(x
+
x0)
+ a0 |
| thus,
y
+ 3
=
-1·
(x
+
1)3
+
3 · (x
+
1)2
-
5
· (x
+
1)
+
6 =>
y
=
-
x3 -
2x
the source
function. |
| Let
prove that the source cubic is an odd function, which means
that f (x)
=
-
f (-x), |
| As
f
(x)
=
-
x3 -
2x
then
-
f (-x)
=
- [-
(-x)3
-
2(-x)]
=
- [
x3
+ 2x]
=
-
x3 -
2x. |
| As
a3a1 > 0
given function is of the type 2/1. |
| Since given function is symmetric to its
point of inflection, and as the y-intercept
a0
=
6, then the x-intercept
or zero of the function must be at the point (2,
0). |
| Therefore,
-
x3
+ 3x2
-
5x
+
6
= -1(x
-
2)(x2
-
x
+
3) |
 |
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|