|
| Conic
Sections |
|
|
|
|
Parabola
and Line
|
Polar of the parabola
|
|
Construction of the tangent at the point on the parabola
|
|
Construction of the tangents from a point exterior to the parabola
|
|
Parabola and line, examples |
|
|
|
|
|
|
| Polar of the parabola
|
|
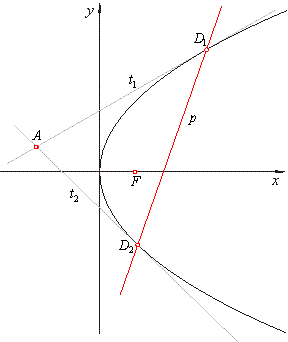
The polar p
of a point A(x0, y0), exterior to the parabola
y2 = 2px, is the secant through the contact
points of the
tangents drawn from the point A
to the parabola. |
|
The tangency points
D1(x1, y1)
and D2(x2, y2)
and the point A
satisfy the equations of tangents,
|
|
t1
:: y1y0
= p(x0
+ x1)
and t2
::
y2y0
= p(x0
+ x2).
|
|
Subtracting
t2
-
t1,
|
|
y0(y2
-
y1)
= p[(x0
+ x2)
- (x0
+ x1)]
|
|
|
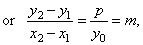
obtained is the slope of the polar. By plugging the slope into equation of the line through the given point
|
 |
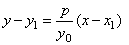or
y0y
= y1y0
+ px -
px1 |
|
|
since y1y0
= p(x0
+ x1),
|
| then
|
y0y
= p(x
+ x0) |
the
equation of the
polar.
|
|
|
 |
|
|
|
Construction of the tangent at the point on the parabola
|
As the vertex of the parabola is the midpoint of the line
segment whose endpoints are, the projection P1'
of the given point to the axis of the parabola and the point
B
opposite it, draw the tangent through points B and P1.
|
|
|
|
Construction of the tangents from a point exterior to the parabola
|
|
Draw the circle centered at the point A
outside the
parabola through the focus.
|
|
The circle intersects the directrix at
points, D1
and D2.
|
Tangents from the point
A
are then perpendicular
bisectors of the line segments, D1F
and D2F.
|
|
Thus, the tangency points,
P1
and P2
are equidistant from the focus and the directrix.
|
|
 |
|
|
| Parabola and line, examples |
| Example:
Find the angle between tangents drawn at intersection points of a line and the parabola
y2 = 2px
if the line passes through the focus F(7/4,
0) and its slope
m =
4/3. |
|
Solution:
As F(p/2,
0)
then, p/2 =
7/4 and the equation
of the parabola y2 =
7x.
|
| By plugging
m =
4/3 and
F(7/4,
0) into
the equation of the line
y
-
y1 =
m(x
-
x1)
obtained is
|
|
|
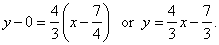
Intersections of the line and the parabola,
|
|
|
 |
|
|
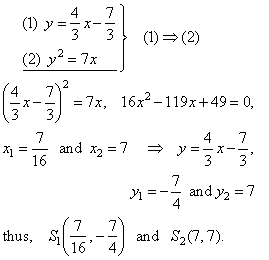
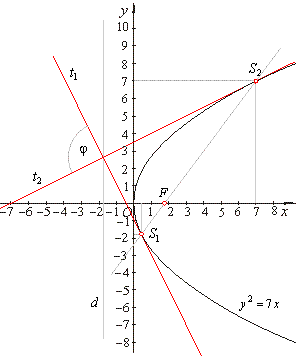Substituting
coordinates of S1
and S2
in
|
 |
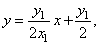we
get the equation of tangents, |
|
 |
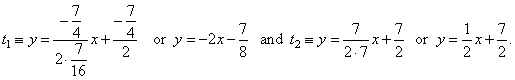| Slopes of tangents satisfy the perpendicularity
condition, |
 |
|
|
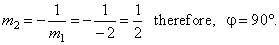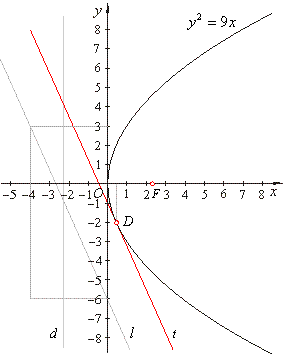
| Example:
Find the point on the parabola
y2 = 9x closest to the line
9x + 4y + 24 =
0. |
|
Solution:
The tangency point of the tangent parallel to
the given line is the closest point.
|
|
9x + 4y +
24 = 0
=> y =
-(9/4)x
-
6, mt =
-
9/4
|
|
The slope of the tangent must satisfy tangency
condition
of the parabola,
|
|
p = 2mc
<= mt =
-
9/4, p
=
9/2
|
|
9/2 = 2 · (-9/4)
· c
=>
c
= -
1
|
|
therefore, the
tangent t
:: y =
-(9/4)x
-
1.
|
|
The solution
to the system of equations of the tangent and the parabola
gives the tangency point, that
is
|
|
|
 |
|
 |
|
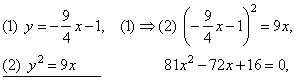
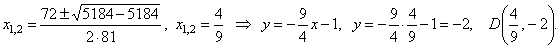| Example:
Given is the polar
4x + y + 12 =
0 of the parabola
y2 = -4x, find coordinates of the pole and
write equations of the corresponding tangents. |
|
Solution:
Intersections of the polar and the parabola are the
tangency points of tangents drawn from the pole P.
Thus, by solving the system of equations of the polar and the parabola
we get the tangency points. |
|
(1) 4x + y +
12 =
0, (1) =>
(2) (-4x
-
12)2 = -4x
|
|
(2) y2 =
-4x
4x2
+ 25x + 36 =
0,
|
|
|
|
|
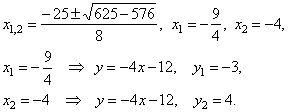
Equation of the tangent at the point on the parabola,
|
|
|
 |
|
|
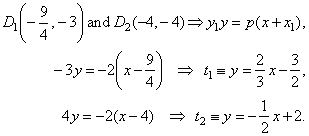
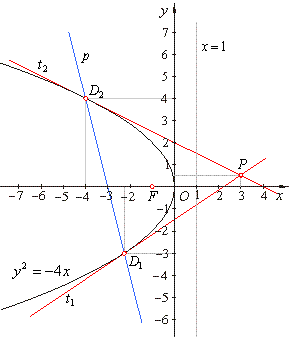The intersection of tangents is the pole P.
Therefore, we solve the system formed by their equations, |
 |
|
|
|
|
|
|
|
|
|
|
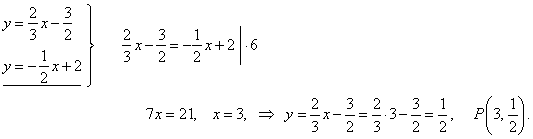| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
