|
|
|
|
Rational
Inequalities |
The
graph of the translated equilateral (or rectangular) hyperbola
|
|
|
|
|
|
|
|
|
The graph of the
translated equilateral (or rectangular) hyperbola
|
|
The graph of the given rational function is translated equilateral (or rectangular)
hyperbola.
|
| A
rational function of the
form
|
 |
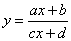can be rewritten into
|
|
|
|
| |
where |
 |
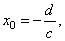the vertical asymptote,
|
 |
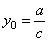the horizontal
asymptote |
|
|
| |
and the
parameter
|
 |
|
|
|
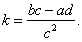Therefore, values of the vertical and
the horizontal asymptote correspond to the coordinates of the horizontal and the vertical translation
of the source
equilateral hyperbola y
= k/x, respectively.
|
| Thus, given rational function |
 |
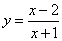where, a
= 1, b
=
-2
and c
=
1,
d
=
1 |
|
| |
has
the vertical asymptote |
 |
|
|
| |
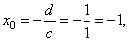the
horizontal asymptote |
 |
|
|
| |
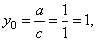and
the parameter |
 |
|
|
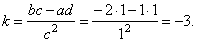| Therefore,
its source function is the equilateral or rectangular
hyperbola |
 |
|
|
|
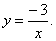The graph of given
rational function is shown below.
|
|
|
|
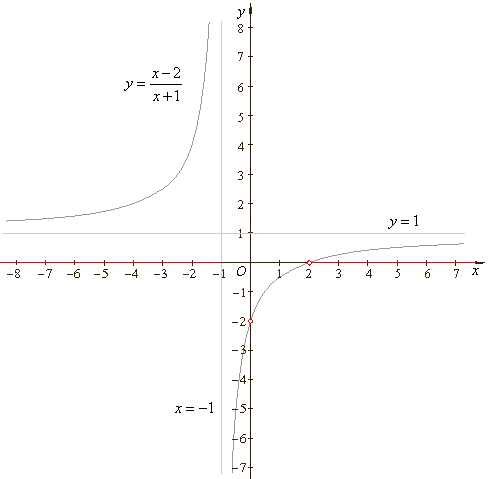
| Example:
Find the solutions
of the inequality
|
|
|
|
|
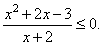
Solution:
The solution set of the given rational inequality includes all numbers
x
which make the inequality less then or equal to 0, or which make the sign of the rational expression
to be negative or 0.
|
|
A rational expression is negative if the numerator and the denominator
have different signs, and the rational expression equals 0 when
its numerator is equal to 0 that is,
|
|
|
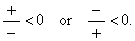
therefore, we have to solve two simultaneous
inequalities.
|
|
We graph the numerator and the
denominator in the same coordinate system to find all points of
the x-axis
that satisfy given inequality.
|
|
The zero points of the numerator and
the denominator divide the x-axis
into four intervals at which given rational expression changes
sign.
|
| x2
+ 2x -
3 = 0, a = 1, b = 2 and
c = -3
|
|
|
|
 |
|
|
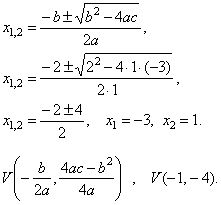
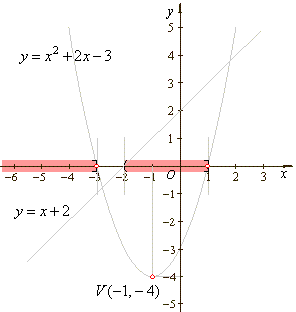The solutions of the two pairs of the simultaneous
inequalities are intersections of sets of their partial solutions,
|
|
|
|
as is shown below.
|
|
|
|
Therefore, the solution set is (-
oo,
- 3]
U
(-
2,
1].
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
|
|
Copyright © 2004 - 2020, Nabla Ltd.
All rights reserved.
|
